| Magnetic Field (Biot-Savert Law): You are continually having troubles with the CRT screen of your computer and wonder if it is due to magnetic fields from the power lines running in your building. A blueprint of the building shows that the nearest power line is as shown below. Your CRT screen is located at point P. Calculate the magnetic field at P as a function of the current I and the distances a and b. Segments BC and AD are arcs of concentric circles. Segments AB and DC are straight-line segments. | 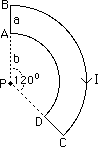 |