Shubnikov de-Haas Oscillations

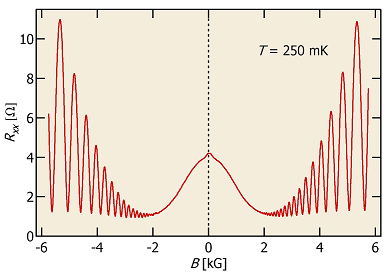
When a 2DES is subject to weak magnetic fields B and low temperatures T, the linear response exhibits oscillations controlled by the ratio of the Fermi energy, E_F, to the cyclotron energy, ħω_c = eB/m [1]. These oscillations are periodic in the inverse magnetic field, 1/B, and are a result of E_F sweeping through the Landau level (LL) energy spectrum. As a LL passes through E_F it depopulates as the electrons become free to flow.

These oscillations are of importance due to their ability to yield information about three important physical parameters. The oscillation frequency, when plotted as a function of 1/B, characterizes the Fermi surface and gives direct examination of the carrier density. Minima of these oscillations occur at integer values of the quantity ν = n_eh/eB, where n_e is the electron density and h and e are fundamental constants. Thus by using adjacent minima one can obtain the carrier density directly.

The other two physical parameters obtained from SdHOs are the effective mass, m*, of the charge carriers and the quantum lifetime, τ_q. Theoretically the amplitude of these oscillations is given by

Δρ_SdHO = 4ρ₀δcos(πν)X(T)/sinhX(T)

where ρ₀ is the resistance at zero magnetic field and X(T) = 2π²T/ω_c. By performing a temperature dependent study of SdHOs one can extract m* [2] from the thermal damping factor and performing a Dingle analysis yields the value of τ_q [3].

Fig. 1 This figure depicts typical form of SdHOs in our 2DESs as obtained in sweeping magnetic field with no external excitation at T = 250 mK.

References

[1] L. Shubnikov and W. de Haas, Leiden Communication 207a, 3 (1930)

[2] P. T. Coleridge, M. Hayne, P. Zawadzki, and A. S. Sachrajda, “Effective masses in high-mobility 2D electron gas structures”, Surface Science 361, 560 (1996) [abstract] [full text]

[3] P. T. Coleridge, R. Stoner, and R Fletcher, “Low-Field Transport Coefficients in GaAs/Ga_1-xAl_xAs Heterostructures&rduo;, Physical Review B 39, 1120 (1989) [abstract] [full text]