LABORATORY II
DESCRIPTION OF MOTION IN TWO DIMENSIONS

This laboratory allows you to continue your study of accelerated motion that you started in the Laboratory I, only the motion is not as idealized. The gliders you used in Laboratory I were nearly frictionless and moved in only one dimension. Motion is more complicated in the real world. Friction and air resistance are important parts of our everyday lives. For example, without friction we could not walk or drive a car, and withour air resistance airplanes and parachutes would not work. All of your daily experiences with motion have been influenced by these effects, and in this lab you will make no attempt to limit their effects like you did with the air tracks. Instead you will need to think of how air resistance and friction will affect your results and why we ignore them when working problems in the textbook.

As the title of this lab suggests, you will study objects that move in two dimensions. In general, all the principles of motion that are valid in one dimension are also valid in two and three dimensions, so that the skills you learned in the first lab will be very helpful in this lab. You will study the motion of an object in free fall, an object in projectile motion, and an object moving in a circle.

As always, if you have any questions, please ask your instructor.

OBJECTIVES: After successfully completing this laboratory, you should be able to:

• Determine how the mass of an object in free-fall affects the object's acceleration.
  
• Determine how the horizontal and vertical components of the instantaneous velocity change during the time of a projectile's flight.
  
• Determine how the horizontal and vertical components of the instantaneous acceleration depend on mass during the time of a projectile's flight.
  
• Determine whether an object revolving in a circle with a constant speed has an acceleration.
  

PREPARATION:

Read Fishbane, Gasiorowicz, and Thornton: Chapter 1, section 6; Chapter 2, section 5; and all of Chapter 3. Review your results and procedures from Laboratory I. Before coming to the lab you should be able to:

• Determine instantaneous and average velocities and accelerations from spark tapes.

• Analyze a vector in terms of its components along a set of x- and y- axes.
  
• Add and subtract vectors graphically.
  

PROBLEM #1: MASS AND THE ACCELERATION OF A FREELY-FALLING OBJECT

You have a summer job with the National Park Service. Your boss is investigating the possibility of using cylindrical canisters filled with fire-retarding chemicals to help fight forest fires. The canisters would be dropped by low-flying planes or helicopters. They are specifically designed to split open when they hit the ground, showering the nearby flames with the chemicals. The canisters could contain different chemicals, so they will have different masses. In order to accurately drop the canisters, your boss needs to know if the motion of the canisters will be different if they contain different chemicals. Because you have taken physics, he asks you to begin to solve the problem by determining if the free-fall acceleration of the canisters depends on their mass.

How does the acceleration of a freely-falling object depend on its mass?

EQUIPMENT

The free-fall apparatus lets you create a spark-tape record from a freely falling object. The object you will be using is designed so you can change its mass without changing its shape.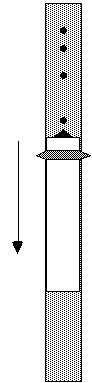

PREDICTION

Make a rough sketch of what you expect the average acceleration-versus-mass graph to look like for freely-falling objects with the same size and shape but different masses.

Do you think the free-fall acceleration increases, decreases, or stays the same as the mass of the object increases? Make your best guess and explain your reasoning.

METHOD QUESTION

Describe how you will determine the acceleration of the object from a spark tape record.

EXPLORATION

In the free-fall apparatus, an electromagnet is switched off to release the object. Without turning on the spark timer, check the vertical alignment of the apparatus to make sure the object falls freely into the sand box (a plumb bob is available). Make sure the object falls into the sandbox, or it will break!

Drop the object several times with the spark timer turned off. Does the falling object interact with anything (other than the Earth) as it falls? Now try changing the object's mass and see how it falls.

DO NOT TOUCH ANYTHING METAL ON THE APPARATUS WHILE THE SPARK TIMER IS IN OPERATION! It operates at 10,000 volts and can give you a nasty shock.

Based on your experiences from Lab I, decide how you intend to determine the average acceleration of the object. Remember, you can only measure the position of the object at specific times. What rate setting on the spark timer yields the best spark record for your purpose?

Perform a few "practice" runs on the first piece of spark paper, making sure you are correctly coordinating the production of sparks and the release of the object.

MEASUREMENT

Measure the mass of the object and make a spark record of it's falling motion using the optimal spark-timer setting. Repeat this procedure for different masses. Make sure you are using your experiences from Lab I to measure the successive positions of the object in the best way.

Analyze your data as you go along (before making the next spark tape), so you can determine how many different spark tapes you need to make, and what the object's mass should be for each tape. Collect enough data to convince yourself and others of your conclusion about how the acceleration of a freely-falling object depends on its mass.

ANALYSIS

In Lab I, Problem #2 (Motion Down an Incline), you analyzed spark tapes using a graphical technique and a numerical technique. Choose one of these techniques (or a combination of graphical and numerical techniques) to determine the acceleration as a function of time from each of your spark records.

How does the acceleration change for each record? Determine the average acceleration of the object in free fall for each value of its mass and make a graph of average acceleration versus the mass.

CONCLUSION

What will you tell your boss? Will the acceleration of a freely-falling canister depend on its mass? State your results in the most general terms supported by your analysis.

Did the data from the spark tapes support your predicted relationship between acceleration and mass. (Make sure you carefully review Appendix D to determine if your data really support this relationship.) If not, what assumptions did you make that were incorrect? Explain your reasoning.

What are the limitations on the accuracy of your measurements and analysis?

PROBLEM #2: PROJECTILE MOTION AND VELOCITY

You have been hired by a toy company. Your group's project is to produce a video tape that guarantees to teach people how to juggle with anything they can pick up - or double their money back. As part of the project, you have been assigned the task of determining the motion of objects that might be thrown by would-be jugglers. To solve this problem, you build a device to launch objects in front of a measurement grid. You know that the motion of a projectile can be expressed in terms of its horizontal and vertical components of velocity. You decide to measure the projectile motion of the test objects to determine how these components change with time.

1. How does the horizontal component of the object's velocity change with time? 2. How does the vertical component of the object's velocity change with time?

EQUIPMENT

A catapult launches an object with a light bulb in its center through the air in front of a grid. A camera takes a "stroboscopic photograph" of the light bulb in flight. The photo looks like a two-dimensional spark record of its motion. That is, the photo shows the position of the object at several successive, equal time intervals.

PREDICTION

1. Make a rough sketch of what you expect the graph of the horizontal velocity component versus time to look like for the object.
Do you think the horizontal component of the object's velocity changes during its flight? If so, how does it change? Or do you think it is constant (does not change)? Make your best guess and explain your reasoning.

2. Make a rough sketch of what you expect the graph of the vertical velocity component versus time to look like for the object.
Do you think the vertical component of the object's velocity changes during its flight? If so, how does it change? Or do you think it is constant (does not change)? Explain your reasoning.

METHOD QUESTIONS

The following questions may help with the prediction and the analysis of your data.

1. What do you expect the stroboscopic photograph of the light bulb's motion to look like? Make a large (about one-half page) rough sketch and explain your reasoning. Be sure to label the horizontal and vertical axes of your sketch. Connect your points with a dotted line or curve to show the expected path of the object.

2. Looking at your sketch, what do you expect a graph of the object's horizontal position versus time to look like? The object's vertical position-versus-time graph? Make rough drawings of these graphs and explain your reasoning.

3. On your original sketch, draw the expected velocity vectors (relative sizes and directions) for several interesting positions, including the maximum height. Explain your reasoning. Decompose each velocity vector into its vertical and horizontal component.

You can now use your sketch of the velocity components as well as your horizontal and vertical position-versus-time graphs to complete your prediction for this problem.

EXPLORATION

Before taking any photos, try launching the object under various conditions. Make sure that one of the group catches the object or it will break on impact with the floor.

Determine the catapult and camera configurations which result in a trajectory that is within the limits of the grid and field of view of the camera, while keeping the object as near as possible to the grid. Why is it important to keep the object's trajectory near the grid?

The background grid must be clearly visible in your photograph. In order to achieve this, you will have to hold the shutter open for a while, either before or after the launch.

MEASUREMENT

Select your best launch conditions and take a photograph. See a group which has already taken a successful picture (or your lab instructor) for the best camera settings to get a good picture.

SOME PEOPLE FIND THE DEVELOPING FLUID FOR THE FILM IRRITATING TO THE SKIN. Be sure to follow the instructions in Appendix A about how to develop your film.

Using the image of the grid on the photograph, choose a convenient coordinate system for determining both the horizontal and vertical position of the object as a function of time.

Record the distance between the camera and the grid, and between the catapult and the grid. Also note the height of the camera's lens relative to the base of the grid. If necessary, these quantities can be used to more accurately obtain the object's position from the photograph.

ANALYSIS

Make graphs of position versus time for both the vertical and horizontal components of the object's motion.

Select an appropriate analysis technique to determine the instantaneous velocity components. Make graphs of the velocity versus time for both horizontal and vertical components of the object's motion.

CONCLUSION

What will you report to your group? How does the horizontal component of a juggled object's velocity depend on time? How does the vertical component of a juggled object's velocity depend on time? State your results in the most general terms supported by your analysis.

Did your measurements agree with your initial predictions? Why or why not? What are the limitations on the accuracy of your measurements and analysis?

PROBLEM #3: PROJECTILE MOTION AND MASS

You have been hired by a toy company. Your group's project is to produce a video tape that guarantees to teach people how to juggle with anything they can pick up -- or double their money back. As part of the project, you have been assigned the task of determining the motion of objects that might be thrown by would-be jugglers. Since people will attempt to juggle things of all sizes and weights, you need to know how the mass of an object will affect how it will move when juggled. You especially need to know if heavier object will fall faster than a lighter object when juggled. To solve this problem, you build a device to launch objects in front of a measurement grid, and measure how the horizontal and vertical components of the acceleration change with time.

1. How does the horizontal component of the object's acceleration depend on its mass? 2. How does the vertical component of the object's acceleration depend on its mass?

EQUIPMENT

If you have done Problem #2, you can skip this section.

A catapult launches an object with a light bulb in its center through the air in front of a grid. A camera takes a "stroboscopic photograph" of the light bulb in flight. The photo looks like a two-dimensional spark record of its motion. That is, the photo shows the position of the object at several successive, equal time intervals. The mass of the object can be changed without changing its shape.

PREDICTIONS

1. Make a rough sketch of what you expect the graph of the horizontal component of acceleration versus mass to look like for objects with different masses.

Do you think the horizontal component of the object's acceleration will increase, decrease, or stay the same as the mass of the object increases? Explain your reasoning.

2. Make a rough sketch of what you expect the graph of the vertical component of acceleration versus mass to look like for objects with different masses.

Do you think the vertical component of the object's acceleration will increase, decrease, or stay the same as the mass of the object increases? Explain your reasoning.

METHOD QUESTIONS

The following questions may help with the prediction and the analysis of your data.

If you have done Problem #2, skip Questions 1 - 3.

1. What do you expect the stroboscopic photograph of the light bulb's motion to look like? Make a large (about one-half page) rough sketch and explain your reasoning. Be sure to label the horizontal and vertical axes of your sketch. Connect your points with a dotted line or curve to show the expected path of the object.

2. Draw the expected velocity vectors (relative sizes and directions) for several interesting positions on your sketch, including the maximum height. Explain your reasoning. Decompose each velocity vector into its vertical and horizontal components.

3. Looking at your sketch, what do you expect a graph of the object's horizontal position versus time to look like? The object's vertical position-versus-time graph? Make rough drawings of these graphs and explain your reasoning. Do the same for the horizontal and vertical components of the object's instantaneous velocity.

4. On your original sketch, draw the expected acceleration vectors at each of your selected positions, including the maximum height. Explain your reasoning.

5. What do you expect a graph of the object's horizontal acceleration versus time to look like? The object's vertical acceleration-versus-time graph? Make rough drawings of these graphs and explain your reasoning.

Now you can make your prediction for this problem. How do you expect the horizontal and vertical components of the object's acceleration to change as the mass of the object changes?

Each group will determine the horizontal and vertical acceleration for a different mass and report their findings to the class. You should be able to draw a sketch of the horizontal and vertical components of the acceleration vs. mass of the object from the data collected by the class.

EXPLORATION

If you have done Problem #2, this exploration is a review. You need only do what you feel is necessary.

Before taking any photos, try launching the object under various conditions. Make sure that one of the group catches the object or it will break on impact with the floor.

Determine the catapult and camera configurations which result in a trajectory that is within the limits of the grid and field of view of the camera, while keeping the object as near as possible to the grid. Why is it important to keep the object's trajectory near the grid? What is the range of masses for the object that give a satisfactory flight?

The background grid must be clearly visible in your photograph. In order to achieve this, you will have to hold the shutter open for a while, either before or after the launch.

MEASUREMENT

Select the mass of the projectile for your group. Be sure that it is a different mass from those selected by other groups in the class.

If you have done Problem #2, the remaining instructions are a review.

Select your best launch conditions and take a photograph. See a group which has already taken a successful picture (or your lab instructor) for the best camera settings to get a good picture.

SOME PEOPLE FIND THE DEVELOPING FLUID FOR THE FILM IRRITATING TO THE SKIN. Be sure to follow the instructions in Appendix A about how to develop your film.

Using the image of the grid on the photograph, choose a convenient coordinate system for determining both the horizontal and vertical position of the object as a function of time.

Record the distance between the camera and the grid, and between the catapult and the grid. Also note the height of the camera's lens relative to the base of the grid. If necessary, these quantities can be used to more accurately obtain the object's position from the photograph.

ANALYSIS

Make graphs of position versus time for both the vertical and horizontal components of the object's motion. Do they agree with your initial predictions? If not, why not?

Select an appropriate analysis technique to determine the instantaneous velocity and instantaneous acceleration components from your position and time data. Make graphs of the horizontal and vertical components of the object's instantaneous velocity and instantaneous acceleration versus time. Were the relative position of the camera, grid and object relevant?

Report your values of your object's mass (with uncertainty) and its horizontal and vertical accelerations as a function of time to the class. Also report the object's average acceleration components (with uncertainties) to the class, and record the values from other groups. Make graphs of horizontal and vertical acceleration versus object mass.

CONCLUSION

What will you report to your group? How does the horizontal component of a juggled object's acceleration depend on time? How does the vertical component of a juggled object's acceleration depend on time? State your results in the most general terms supported by your analysis.

Did your measurements agree with your initial predictions? Why or why not? How does your conclusion tie together with your results from previous laboratory problems? What are the limitations on the accuracy of your measurements and analysis?

PROBLEM #4: A VECTOR APPROACH TO CIRCULAR MOTION

Because of your physics background and your experience with carnival rides, you have been appointed to a Citizen Committee for the Mall of America's Camp Snoopy. The Committee is writing a report about the safety of a proposed new ride called "The Spinner." Several of the Committee members insist that an object moving in a circle at constant speed is not accelerating, so there is no need to be concerned about the safety of this ride. To help the Committee, you borrow a "Spinner" from the physics department so you can show them the magnitude and direction of the acceleration.

What is the magnitude and direction of the acceleration for an object moving in a circle with a constant speed?

EQUIPMENT

You will be using the apparatus described in Appendix A. (The apparatus is called the "Spinner.") This apparatus produces a two-dimensional spark record of position versus time for an object with a circular path.

PREDICTION

What is the magnitude and direction of the acceleration for an object moving at a constant speed (V) in a circle of radius R? Why? Explain your reasoning.

METHOD QUESTIONS

As usual, to determine the acceleration, you need to know how the velocity changes with the time. To determine the velocity, you need to know how the position changes with time. The following questions may help with the prediction and the analysis of your data.

1. How will the spark pattern look for an object moving in a circle at a constant speed? Make a large, full page sketch and explain your reasoning.

2. On your sketch, draw a vector that shows the object's change in position between two neighboring dots. Do this for all of the pairs of neighboring dots on your sketch.

3. Construct a vector which represents the direction and magnitude of the object's average velocity between each pair of neighboring dots. At some position between the dots, the object's instantaneous velocity is equal to this average velocity. Put the instantaneous velocity vector where you think this will occur and justify your choice. Repeat this procedure for each pair of neighboring dots.

4. Now you can complete the prediction for this problem. Construct a vector which represents the direction and magnitude of the average acceleration between the positions for which you have determined the object's instantaneous velocities. At some position between these positions, the object's instantaneous acceleration is equal to this average acceleration. Put the instantaneous acceleration vector where you think this will occur and justify your choice. Repeat this procedure for each pair of instantaneous velocities.

EXPLORATION

Practice spinning the object at different speeds. Which speed gives the best results? How many rotations does the apparatus make before it slows down appreciably?

Try spark frequencies which will give a spark pattern which will be satisfactory for your analysis. Do not put tape on the mass support rods!

DO NOT TOUCH ANYTHING METAL ON THE APPARATUS WHILE THE SPARK TIMER IS IN OPERATION! It operates at 10,000 volts and can give you a nasty shock.

MEASUREMENT

Obtain a spark record for the object at the maximum possible radius using a blank sheet of paper. Record both the spark timer frequency and the radius for this motion.

ANALYSIS

Repeat the procedure you used to answer the Method Questions to find the magnitude and direction of the acceleration of the object.

CONCLUSION

What will you show the Committee? What is the magnitude and direction of the acceleration for an object moving with a constant speed in a circle? State your result in the most general terms supported by your analysis.

Is your answer consistent with your predictions? Why or why not?

Check Your Understanding:

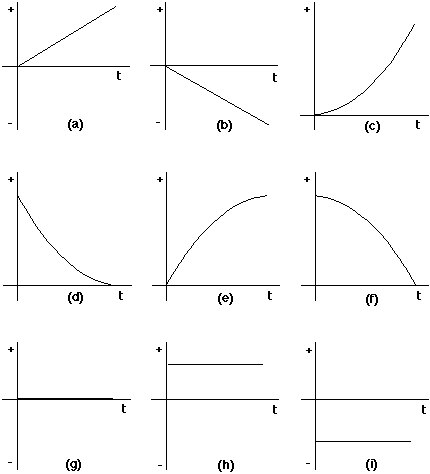
1. A baseball is hit horizontally with an initial velocity vo at time to = 0 and follows the parabolic arc shown at right.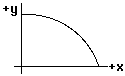

a. Which graph below best represents the horizontal position (x) versus time graph? Explain your reasoning.
b. Which graph below best represents the horizontal velocity (v_x) versus time graph? Explain your reasoning.
c. Which graph below best represents the horizontal acceleration (a_x) versus time graph? Explain your reasoning.
d. Which graph below best represents the vertical position (y) versus time graph? Explain your reasoning.
e. Which graph below best represents the vertical velocity (v_y) versus time graph? Explain your reasoning.

f. Which graph below best represents the vertical acceleration (a_y) versus time graph? Explain your reasoning.

2. Suppose you throw a ball vertically up into the air with an initial velocity v_o.
a. What is the acceleration of the ball at its maximum height? Explain your reasoning.
b. What would the acceleration versus time graph look like from the moment the ball leaves your hand to the moment before it returns to your hand.

3. Two beads are fixed to a rod rotating at constant speed about a pivot at its left end, as shown in the drawing at right.

a. Which bead has the greater speed? Explain your reasoning.
b. Which bead has the centripetal acceleration of greater magnitude? Explain your reasoning.

4. Two racing boats go around a semicircular turn in a race course. The boats have the same speed, but boat A is on the inside while boat B is on the outside, as shown in the drawing.

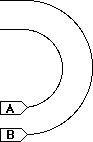
a. Which boat gets around the turn in the smaller time? Explain your reasoning.
b. Which boat undergoes the greater change in velocity while in the turn? Explain your reasoning.
c. Based on the definition of acceleration, which boat has the greater acceleration while in the turn? Explain your reasoning.
d. Based on the equation for centripetal acceleration, which boat has the greater acceleration while in the turn? Compare your answer to part c. Explain your reasoning.

Return to 1251 Labs Table of Contents

Return to Physics Education Home Page

Last Updated: Fri, May 22, 1996 12:00 PM EST