Physics Education Research and Development Group |
Mechanics problems:
- You are writing a short adventure story for your
English class. In your story, two submarines on a
secret mission need to arrive at a place in the
middle of the Atlantic ocean at the same time.
They start out at the same time from positions
equally distant from the rendezvous point. They
travel at different velocities but both go in a
straight line. The first submarine travels at an
average velocity of 20 km/hr for the first 500
km, 40 km/hr for the next 500 km, 30 km/hr for
the next 500 km and 50 km/hr for the final 500
km. In the plot, the second submarine is required
to travel at a constant velocity, so the captain
needs to determine the magnitude of that
velocity.
- It is a beautiful weekend day and, since winter
will soon be here, you and four of your friends
decide to spend it outdoors. Two of your friends
just want to relax while the other two want some
exercise. You need some quiet time to study. To
satisfy everyone, the group decides to spend the
day on the river. Two people will put a canoe in
the river and just drift downstream with the 1.5
mile per hour current. The second pair will begin
at the same time as the first from 10 miles
downstream. They will paddle upstream until the
two canoes meet. Since you have been canoeing
with these people before, you know that they will
have an average velocity of 2.5 miles per hour
relative to the shore when they go against this
river current. When the two canoes meet, they
will come to shore and you should be there to
meet them with your van. You decide to go to that
spot ahead of time so you can study while you
wait for your friends. Where will you wait?
- It's a sunny Sunday afternoon, about 65 °F, and
you are walking around Lake Calhoun enjoying the
last of the autumn color. The sidewalk is crowded
with runners and walkers. You notice a runner
approaching you wearing a tee-shirt with writing
on it. You read the first two lines, but are
unable to read the third and final line before he
passes. You wonder, "Hmm, if he continues
around the lake, I bet I'll see him again, but I
should anticipate the time when we'll pass
again." You look at your watch and it is
3:07 p.m. You recall the lake is 3.4 miles in
circumference. You estimate your walking speed at
3 miles per hour and the runner's speed to be
about 7 miles per hour.
- You have joined the University team racing a
solar powered car. The optimal average speed for
the car depends on the amount of sun hitting its
solar panels. Your job is to determine strategy
by programming a computer to calculate the car's
average speed for a day consisting of different
race conditions. To do this you need to determine
the equation for the day's average speed based on
the car's average speed for each part of the
trip. As practice you imagine that the day's race
consists of some distance under bright sun, the
same distance with partly cloudy conditions, and
twice that distance under cloudy conditions.
- Because of your technical background, you have
been given a job as a student assistant in a
University research laboratory that has been
investigating possible accident avoidance systems
for oil tankers. Your group is concerned about
oil spills in the North Atlantic caused by a
super tanker running into an iceberg. The group
has been developing a new type of down-looking
radar which can detect large icebergs. They are
concerned about its rather short range of 2
miles. Your research director has told you that
the radar signal travels at the speed of light
which is 186,000 miles per second but once the
signal arrives back at the ship it takes the
computer 5 minutes to process the signal.
Unfortunately, the super tankers are such huge
ships that it takes a long time to turn them.
Your job is to determine how much time would be
available to turn the tanker to avoid a collision
once the tanker detects an iceberg. A typical
sailing speed for super tankers during the winter
on the North Atlantic is about 15 miles per hour.
Assume that the tanker is heading directly at an
iceberg that is drifting at 5 miles per hour in
the same direction that the tanker is going.
The following four problems are mathematically equivalent, with different contexts.
- You and your friend run outdoors at least 10
miles every day no matter what the weather (well
almost). Today the temperature is at a brisk 0 oF
with a -20 oF wind chill. Your friend, a real
running fanatic, insists that it is OK to run.
You agree to this madness as long as you both
begin at your house and end the run at her nice
warm house in a way that neither of you has to
wait in the cold. You know that she runs at a
very consistent pace with an average speed of 3.0
m/s, while your average speed is a consistent 4.0
m/s. Your friend finishes warming up first so she
can get a head start. The plan is that she will
arrive at her house first so that she can unlock
the door before you arrive. Five minutes later,
you notice that she dropped her keys. If she
finishes her run first she will have to stand
around in the cold and will not be happy. How far
from your house will you be when you catch up to
her if you leave immediately, run at your usual
pace, and don't forget to take her keys?
- Because of your technical background, you have
been given a job as a student assistant in a
University research laboratory that has been
investigating possible accident avoidance systems
for oil tankers. Your group is concerned about
oil spills in the North Atlantic caused by a
super tanker running into an iceberg. The group
has been developing a new type of down-looking
radar which can detect large icebergs. They are
concerned about its rather short range of 2
miles. Your research director has told you that
the radar signal travels at the speed of light
which is 186,000 miles per second but once the
signal arrives back at the ship it takes the
computer 5 minutes to process the signal.
Unfortunately, the super tankers are such huge
ships that it takes a long time to turn them.
Your job is to determine how much time would be
available to turn the tanker to avoid a collision
once the tanker detects an iceberg. A typical
sailing speed for super tankers during the winter
on the North Atlantic is about 15 miles per hour.
Assume that the tanker is heading directly at an
iceberg that is drifting at 5 miles per hour in
the same direction that the tanker is going.
- Because of your technical background, you have
been given a job as a student assistant in a
University research laboratory that has been
investigating possible accident avoidance systems
for automobiles. You have just begun a study of
how bats avoid obstacles. In your study, a bat is
fitted with a transceiver that broadcasts the
bats velocity to your instruments. Your research
director has told you that the signal travels at
the speed of light which is 1.0 ft/nanosecond (1
nanosecond is 10-9 seconds). You know that the
bat detects obstacles by emitting a forward going
sound pulse (sonar) which travels at 1100 ft/s
through the air. The bat detects the obstacle
when the sound pulse reflect from the obstacle
and that reflected pulse is heard by the bat. You
are told to determine the maximum amount of time
that a bat has after it detects the existence of
an obstacle to change its flight path to avoid
the obstacle. In the experiment your instruments
tell you that a bat is flying straight toward a
wall at a constant velocity of 20.0 ft/s and
emits a sound pulse when it is 10.0 ft from the
wall.
- You have been hired to work in a University
research laboratory assisting in experiments to
determine the mechanism by which chemicals such
as aspirin relieve pain. Your task is to
calibrate your detection equipment using the
properties of a radioactive isotope (an atom with
an unstable nucleus) which will later be used to
track the chemical through the body. You have
been told that your isotope decays by first
emitting an electron and then, some time later,
it emits a photon which you know is a particle of
light. You set up your equipment to determine the
time between the electron emission and the photon
emission. Your apparatus detects both electrons
and photons. You determine that the electron and
photon from a decay arrive at your detector at
the same time when it is 2.0 feet from your
radioactive sample. A previous experiment has
shown that the electron from this decay travels
at one half the speed of light. You know that the
photon travels at the speed of light which is 1.0
foot per nanosecond. A nanosecond is 10-9
seconds.
- You are part of a citizen's group evaluating the
safety of a high school athletic program. To help
judge the diving program you would like to know
how fast a diver hits the water in the most
complicated dive. The coach has his best diver
perform for your group. The diver, after jumping
from the high board, moves through the air with a
constant acceleration of 9.8 m/s2. Later in the
dive, she passes near a lower diving board which
is 3.0 m above the water. With your trusty stop
watch, you determine that it took 0.20 seconds to
enter the water from the time the diver passed
the lower board. How fast was she going when she
hit the water?
- As you are driving to school one day, you pass a
construction site for a new building and stop to
watch for a few minutes. A crane is lifting a
batch of bricks on a pallet to an upper floor of
the building. Suddenly a brick falls off the
rising pallet. You clock the time it takes for
the brick to hit the ground at 2.5 seconds. The
crane, fortunately, has height markings and you
see the brick fell off the pallet at a height of
22 meters above the ground. A falling brick can
be dangerous, and you wonder how fast the brick
was going when it hit the ground. Since you are
taking physics, you quickly calculate the answer.
- Because of your knowledge of physics, you have been
hired as a technical adviser on a new action movie. In one scene, the
hero pursues the villain up to the top of a bungee jump. The villain
creates a diversion by dropping a bottle filled with deadly gas. The
script calls for the hero to quickly strap on a 100 ft. bungee cord and
jump straight down to grab the bottle out of the air just as the bungee
cord begins to stretch. Your job is to determine the feasibility of the
stunt by finding the initial speed with which the hero length needs to
jump downward to catch the bottle. You estimate that the hero can react
to the villain's dropping the bottle by strapping on the bungee cord and
jumping in 2.0 seconds.
- You are helping a friend devise some challenging
tricks for the upcoming Twin Cities Freestyle
Skateboard Competition. To plan a series of
moves, he needs to know the rate that the
skateboard, with him on board, slows down as it
coasts up the competition ramp which is at 30°
to the horizontal. Assuming that this rate is
constant, you decide to have him conduct an
experiment. When he is traveling as fast as
possible on his competition skateboard, he stops
pushing and coasts up the competition ramp. You
measure that he typically goes about 95 feet in 6
seconds. Your friend weighs 170 lbs wearing all
of his safety gear and the skateboard weighs 6
lbs.
- You have a summer job working for a University
research group investigating the causes of the
ozone depletion in the atmosphere. The plan is to
collect data on the chemical composition of the
atmosphere as a function of the distance from the
ground using a mass spectrometer located in the
nose cone of a rocket fired vertically. To make
sure the delicate instruments survive the launch,
your task is to determine the acceleration of the
rocket before it uses up its fuel. The rocket is
launched straight up with a constant acceleration
until the fuel is gone 30 seconds later. To
collect enough data, the total flight time must
be 5.0 minutes before the rocket crashes into the
ground.
- You have landed a summer job as the technical
assistant to the director of an adventure movie
shot here in Minnesota. The script calls for a
large package to be dropped onto the bed of a
fast moving pick-up truck from a helicopter that
is hovering above the road, out of view of the
camera. The helicopter is 235 feet above the
road, and the bed of the truck is 3 feet above
the road. The truck is traveling down the road at
40 miles/hour. You must determine when to cue the
assistant in the helicopter to drop the package
so it lands in the truck. The director is paying
$20,000 per hour for the chopper, so he wants you
to do this successfully in one take.
- Just for the fun of it, you and a friend decide
to enter the famous Tour de Minnesota bicycle
race from Rochester to Duluth and then to St.
Paul. You are riding along at a comfortable speed
of 20 mph when you see in your mirror that your
friend is going to pass you at what you estimate
to be a constant 30 mph. You will, of course,
take up the challenge and accelerate just as she
passes you until you pass her. If you accelerate
at a constant 0.25 miles per hour each second
until you pass her, how long will she be ahead of
you?
- In your new job, you are the technical advisor
for the writers of a gangster movie about Bonnie
and Clyde. In one scene Bonnie and Clyde try to
flee from one state to another. (If they got
across the state line, they could evade capture,
at least for a while until they became Federal
fugitives.) In the script, Bonnie is driving down
the highway at 108 km/hour, and passes a
concealed police car that is 1 kilometer from the
state line. The instant Bonnie and Clyde pass the
patrol car, the cop pulls onto the highway and
accelerates at a constant rate of 2 m/s2. The
writers want to know if they make it across the
state line before the pursuing cop catches up
with them.
- The University Skydiving Club has asked you to
plan a stunt for an air show. In this stunt, two
skydivers will step out of opposite sides of a
stationary hot air balloon 5,000 feet above the
ground. The second skydiver will leave the
balloon 20 seconds after the first skydiver but
you want them both to land on the ground at the
same time. The show is planned for a day with no
wind so assume that all motion is vertical. To
get a rough idea of the situation, assume that a
skydiver will fall with a constant acceleration
of 32 ft/sec2 before the parachute opens. As soon
as the parachute is opened, the skydiver falls
with a constant velocity of 10 ft/sec. If the
first skydiver waits 3 seconds after stepping out
of the balloon before opening her parachute, how
long must the second skydiver wait after leaving
the balloon before opening his parachute?
- Because parents are concerned that children are
learning "wrong" science from TV, you
have been asked to be a technical advisor for a
science fiction cartoon show on Saturday morning.
In the plot, a vicious criminal (Natasha Nogood)
escapes from a space station prison. The prison
is located between galaxies far away from any
stars. Natasha steals a small space ship and
blasts off to meet her partners somewhere in deep
space. The stolen ship accelerates in a straight
line at its maximum possible acceleration of 30
m/sec2. After 10 minutes all of the fuel is
burned up and the ship coasts at a constant
velocity. Meanwhile, the hero (Captain Starr)
learns of the escape while dining in the prison
with the warden's daughter (Virginia Lovely). Of
course he immediately (as soon as he finishes
dessert) rushes off the recapture Natasha. He
gives chase in an identical ship, which has an
identical maximum acceleration, going in an
identical direction. Unfortunately, Natasha has a
30 minute head start. Luckily, Natasha's ship did
not start with a full load of fuel. With his full
load of fuel, Captain Starr can maintain maximum
acceleration for 15 minutes. How long will it
take Captain Starr's ship to catch up to
Natasha's?
- Because parents are concerned that children are
learning "wrong" science from TV, you
have been asked to be a technical advisor for a
new science fiction show. The show takes place on
a space station at rest in deep space far away
from any stars. In the plot, a vicious criminal
(Alicia Badax) escapes from the space station
prison. Alicia steals a small space ship and
blasts off to meet her partners somewhere in deep
space. If she is to just barely escape, how long
do her partners have to transport her off her
ship before she is destroyed by a photon torpedo
from the space station? In the story, the stolen
ship accelerates in a straight line at its
maximum possible acceleration of 30 m/sec2. After
10 minutes (600 seconds) all of the fuel is
burned and the ship coasts at a constant
velocity. Meanwhile, the hero of this episode
(Major Starr) learns of the escape while dining
with the station's commander. Of course she
immediately rushes off to fire photon torpedoes
at Alicia. Once fired, a photon torpedo travels
at a constant velocity of 20,000 m/s. By that
time Alicia has a 30 minute (1800 seconds) head
start on the photon torpedo.
- You want to visit your friend in Seattle and decide to
take the train. Unfortunately, you are late getting to the train
station. You are running as fast as you can, but 30 meters ahead of you
the train begins to pull out. You can run at a maximum speed of 8 m/s
and the train is accelerating at 1 m/s/s. In 50 meters you will reach a
barrier. Can you catch up to your train?
- Because of your knowledge of physics, you have
been assigned to investigate a train wreck
between a fast moving passenger train and a
slower moving freight train both going in the
same direction. You have statements from the
engineer of each train and the stationmaster as
well as some measurements which you make. To
check the consistency of each person's
description of the events leading up to the
collision, you decide to calculate the distance
from the station that the collision should have
occurred if everyone were telling what really
happened and compare that with the actual
position of the wreck which is 0.5 miles from the
station. In this calculation you decide that you
can ignore all reaction times. Here is what you
know:
- The stationmaster claims that she noted that the freight train was behind schedule. As regulations require, she switched on a warning light just as the last car of the freight train passed her.
- The freight train engineer says he was going at a constant speed of 10 miles per hour.
- The passenger train engineer says she was going at the speed limit of 40 miles per hour when she approached the warning light. Just as she reached the warning light she saw it go on and immediately hit the brakes.
- The warning light is located so that a train gets to it 2.0 miles before it gets to the station.
- The passenger train slows down at a constant rate of 1.0 mile per hour for each minute as soon as you hit the brakes.
DO ONLY THE PROBLEM SOLVING STEPS NECESSARY TO FOCUS THE PROBLEM AND DESCRIBE THE PHYSICS OF THE PROBLEM. DO NOT SOLVE THIS PROBLEM.
- While on a vacation to Kenya, you visit the port
city of Mombassa on the Indian Ocean. On the
coast you find an old Portuguese fort probably
built in the 16th century. Large stone walls rise
vertically from the shore to protect the fort
from cannon fire from pirate ships. Walking
around on the ramparts, you find the fort's
cannons mounted such that they fire horizontally
out of holes near the top of the walls facing the
ocean. Leaning out of one of these gun holes, you
drop a rock which hits the ocean 3.0 seconds
later. You wonder how close a pirate ship would
have to sail to the fort to be in range of the
fort's cannon? Of course you realize that the
range depends on the velocity that the cannonball
leaves the cannon. That muzzle velocity depends,
in turn, on how much gunpowder was loaded into
the cannon. (a) Calculate the muzzle velocity
necessary to hit a pirate ship 300 meters from
the base of the fort. (b) To determine how the
muzzle velocity must change to hit ships at
different positions, make a graph of horizontal
distance traveled by the cannonball (range)
before it hits the ocean as a function of muzzle
velocity of the cannonball for this fort.
- Because of your knowledge of physics, you
have been hired as a consultant for a new
James Bond movie, "Oldfinger".
In one scene, Bond jumps horizontally off
the top of a cliff to escape a villain.
To make the stunt more dramatic, the
cliff has a horizontal ledge a distance h
beneath the top of the cliff which
extends a distance L from the vertical
face of the cliff. The stunt coordinator
wants you to determine the minimum
horizontal speed, in terms of L and h,
with which Bond must jump so that he
misses the ledge.
- Because of your knowledge of physics, you
have been hired as a consultant for a new
James Bond movie, "Oldfinger".
In one scene, Bond jumps horizontally off
the top of a cliff to escape a villain.
To make the stunt more dramatic, the
cliff has a horizontal ledge a distance h
beneath the top of the cliff which
extends a distance L from the vertical
face of the cliff. The stunt coordinator
wants you to determine the minimum
horizontal speed, in terms of L and h,
with which Bond must jump so that he
misses the ledge.
- You are on the target range preparing to shoot a
new rifle when it occurs to you that you would
like to know how fast the bullet leaves the gun
(the muzzle velocity). You bring the rifle up to
shoulder level and aim it horizontally at the
target center. Carefully you squeeze off the shot
at the target which is 300 feet away. When you
collect the target you find that your bullet hit
9.0 inches below where you aimed.
- You have a great summer job working on
the special effects team for a Minnesota
movie, the sequel to Fargo. A body is
discovered in a field during the fall
hunting season and the sheriff begins her
investigation. One suspect is a hunter
who was seen that morning shooting his
rifle horizontally in the same field. He
claims he was shooting at a deer and
missed. You are to design the
“flashback” scene which shows
his version of firing the rifle and the
bullet kicking up dirt where it hits the
ground. The sheriff later finds a bullet
in the ground. She tests the hunter's
rifle and finds the velocity that it
shoots a bullet (muzzle velocity). In
order to satisfy the nitpickers who
demand that movies be realistic, the
director has assigned you to calculate
the distance from the hunter that this
bullet should hit the ground as a
function of the bullet's muzzle velocity
and the rifle's height above the ground.
- You have a great summer job working on
the special effects team for a Minnesota
movie, the sequel to Fargo. A body is
discovered in a field during the fall
hunting season and the sheriff begins her
investigation. One suspect is a hunter
who was seen that morning shooting his
rifle horizontally in the same field. He
claims he was shooting at a deer and
missed. You are to design the
“flashback” scene which shows
his version of firing the rifle and the
bullet kicking up dirt where it hits the
ground. The sheriff later finds a bullet
in the ground. She tests the hunter's
rifle and finds the velocity that it
shoots a bullet (muzzle velocity). In
order to satisfy the nitpickers who
demand that movies be realistic, the
director has assigned you to calculate
the distance from the hunter that this
bullet should hit the ground as a
function of the bullet's muzzle velocity
and the rifle's height above the ground.
- The Police Department has hired you as a consultant in
a robbery investigation. A thief allegedly robbed a bank and, to escape
the pursing security guards, took the express elevator to the roof of
the building. Then, in order to not be caught with the evidence, the
thief allegedly threw the money bag to a waiting accomplice on the roof
of the next building. The defense attorney contends that in order to
reach the roof of that next building, the defendant would have had to
throw the money bag horizontally with a minimum velocity of 10
meters/second. However, in a test, the accused could throw the bag with
a maximum horizontal velocity of no more than 5 meters/second. How will
you advise the prosecuting attorney? You determine that the bank
building is 250 meters high, the next building is 100 meters high and
the distance between them is 20 meters.
- You are watching people practicing archery when
you wonder how fast an arrow is shot from a bow.
With a flash of insight you remember your physics
and see how you can easily determine what you
want to know by a simple measurement. You ask one
of the archers to pull back her bow string as far
as possible and shoot an arrow horizontally. The
arrow strikes the ground at an angle of 86
degrees from the vertical at 100 feet from the
archer.
- You read in the newspaper that rocks from Mars
have been found on Earth. Your friend says that the rocks were shot off
Mars by the large volcanoes there. You are skeptical so you decide to
calculate the magnitude of the velocity that volcanoes eject rocks from
geological evidence. You know the gravitational acceleration of objects
falling near the surface of Mars is only 40% that on the Earth. You can
look up the height of Martian volcanoes and determine the distance rocks
from a volcano hit the ground from pictures of the Martian surface. If
you assume the rocks farthest from a volcano were ejected at an angle of
45 degrees, what is the magnitude of the rock's velocity as a function
of its distance from the volcano and the height of the volcano for the
rock furthest from the volcano?
- You read in the newspaper that rocks from Mars
have been found on Earth. Your friend says that the rocks were shot off
Mars by the large volcanoes there. You are skeptical so you decide to
calculate the magnitude of the velocity that volcanoes eject rocks from
geological evidence. You know the gravitational acceleration of objects
falling near the surface of Mars is only 40% that on the Earth. You can
look up the height of Martian volcanoes and determine the distance rocks
from a volcano hit the ground from pictures of the Martian surface. If
you assume the rocks farthest from a volcano were ejected at an angle of
45 degrees, what is the magnitude of the rock's velocity as a function
of its distance from the volcano and the height of the volcano for the
rock furthest from the volcano?
- Watching the world series (only as an example of
physics in action), you wonder about the ability
of the catcher to throw out a base runner trying
to steal second. Suppose a catcher is crouched
down behind the plate when he observes the runner
breaking for second. After he gets the ball from
the pitcher, he throws as hard as necessary to
second base without standing up. If the catcher
throws the ball at an angle of 30 degrees from
the horizontal so that it is caught at second
base at about the same height as that catcher
threw it, how much time does it take for the ball
to travel the 120 feet from the catcher to second
base?
- Because of your physics background, you
have been hired as a consultant for a new
movie about Galileo. In one scene, he
climbs up to the top of a tower and, in
frustration over the people who ridicule
his theories, throws a rock at a group of
them standing on the ground. The rock
leaves his hand at 30° from the
horizontal. The script calls for the rock
to land 15 m from the base of the tower
near a group of his detractors. It is
important for the script that the rock
take precisely 3.0 seconds to hit the
ground so that there is time for a good
expressive close-up. The set coordinator
is concerned that the rock will hit the
ground with too much speed causing cement
chips from the plaza to injure one of the
high priced actors. You are told to
calculate that speed.
- Because of your physics background, you
have been hired as a consultant for a new
movie about Galileo. In one scene, he
climbs up to the top of a tower and, in
frustration over the people who ridicule
his theories, throws a rock at a group of
them standing on the ground. The rock
leaves his hand at 30° from the
horizontal. The script calls for the rock
to land 15 m from the base of the tower
near a group of his detractors. It is
important for the script that the rock
take precisely 3.0 seconds to hit the
ground so that there is time for a good
expressive close-up. The set coordinator
is concerned that the rock will hit the
ground with too much speed causing cement
chips from the plaza to injure one of the
high priced actors. You are told to
calculate that speed.
- While watching a softball game you see a play that
makes you wonder how fast a fielder can to react to a hit, run to the
fence, and leap up to make the catch. In this play, the batter hits a
ball when it is barely off the ground. It looks like a home run over the
left center field wall which is 200 ft from home plate. As soon as the
ball is hit, the left fielder runs to the wall, leaps high, and catches
the it just before it clears the top of 10 ft high wall. You estimate
that the ball left the bat at an angle of 30 degrees.
- You are still a member of a citizen's committee
investigating safety in the high school sports
program. Now you are interested in knee damage to
athletes participating in the long jump
(sometimes called the broad jump). The coach has
her best long jumper demonstrate the event for
you. He runs down the track and, at the take-off
point, jumps into the air at an angle of 30
degrees from the horizontal. He comes down in a
sand pit at the same level as the track 26 feet
away from his take-off point. With what velocity
(both magnitude and direction) did he hit the
ground?
- In your new job, you are helping to design stunts
for a new movie. In one scene the writers want a
car to jump across a chasm between two cliffs.
The car is driving along a horizontal road when
it goes over one cliff. Across the chasm, which
is 1000 feet deep, is another road at a lower
height. They want to know the minimum value of
the speed of the car so that it does not fall
into the chasm. They have not yet selected the
car so they want an expression for the speed of
the car, v, in terms of the car's mass, m, the
width of the chasm, w, and the height of the
upper road, h, above the lower road. The stunt
director will plug in the actual numbers after a
car is purchased.
- Your friend has decided to make some money during
the next State Fair by inventing a game of skill
that can be installed in the Midway. In the game
as she has developed it so far, the customer
shoots a rifle at a 5.0 cm diameter target
falling straight down. Anyone who hits the target
in the center wins a stuffed animal. Each shot
would cost 50 cents. The rifle would be mounted
on a pivot 1.0 meter above the ground so that it
can point in any direction at any angle. When
shooting, the customer stands 100 meters from
where the target would hit the ground if the
bullet misses. At the instant that the bullet
leaves the rifle (with a muzzle velocity of 1200
ft/sec according to the manual), the target is
released from its holder 7.0 meters above the
ground. Your friend asks you to try out the game
which she has set up on a farm outside of town.
Before you fire the gun you calculate where you
should aim.
- You have a summer job with an insurance company
and have been asked to help with the
investigation of a tragic "accident."
When you visit the scene, you see a road running
straight down a hill which has a slope of 10
degrees to the horizontal. At the bottom of the
hill, the road goes horizontally for a very short
distance becoming a parking lot overlooking a
cliff. The cliff has a vertical drop of 400 feet
to the horizontal ground below where a car is
wrecked 30 feet from the base of the cliff. Was
it possible that the driver fell asleep at the
wheel and simply drove over the cliff? After
looking pensive, your boss tells you to calculate
the speed of the car as it left the top of the
cliff. She reminds you to be careful to write
down all of your assumptions so she can evaluate
the applicability of the calculation to this
situation. Obviously, she suspects foul play.
- At your job with an insurance company, you have been
asked to help with the investigation of a tragic "accident." At the
scene is a road that runs straight down a hill with a slope of 10
degrees below the horizontal. At the bottom of the hill, the road goes
horizontally for a very short distance, then ends in a parking lot
overlooking a cliff. The cliff has a vertical drop of 400 feet to the
horizontal ground below where the wrecked car lies 30 feet from the base
of the cliff. The only witness claims that the car was parked somewhere
on the hill, he can't exactly remember where, and the car just began
coasting down the road. The witness did not hear an engine and thinks
that the driver was drunk and passed out knocking off his emergency
brake. The witness also remembers that the car took about 3 seconds to
get down the hill. The lead investigator drops a stone from the edge of
the cliff and, from the sound of it hitting the ground below, determines
that it takes 5.0 seconds to fall to the bottom. Based on that
information, you are told to calculate the car's average acceleration
coming down the hill using the statement of the witness and the other
facts in the case. You are reminded to write down all of your
assumptions so the investigation team can evaluate the applicability of
your calculation to this situation.
- Your group has been selected to serve on a
citizen's panel to evaluate a new proposal to
search for life on Mars. On this unmanned
mission, the lander will leave orbit around Mars
falling through the atmosphere until it reaches
10,000 meters above the surface of the planet. At
that time a parachute opens and takes the lander
down to 500 meters. Because of the possibility of
very strong winds near the surface, the parachute
detaches from the lander at 500 meters and the
lander falls freely through the thin Martian
atmosphere with a constant acceleration of 0.40g
for 1.0 second. Retrorockets then fire to bring
the lander to a softly to the surface of Mars. A
team of biologists has suggested that Martian
life might be very fragile and decompose quickly
in the heat from the lander. They suggest that
any search for life should begin at least 9
meters from the base of the lander. This biology
team has designed a probe which is shot from the
lander by a spring mechanism in the lander 2.0
meters above the surface of Mars. To return the
data, the probe cannot be more than 11 meters
from the bottom of the lander. Combining the data
acquisition requirements with the biological
requirements the team designed the probe to enter
the surface of Mars 10 meters from the base of
the lander. For the probe to function properly it
must impact the surface with a velocity of 8.0
m/s at an angle of 30 degrees from the vertical.
Can this probe work as designed?
- You have been hired as a technical
consultant for a new action movie. The
director wants a scene in which a car
goes up one side of an open drawbridge,
leaps over the gap between the two sides
of the bridge, and comes down safely on
the other side of the bridge. This
drawbridge opens in the middle by
increasing the angle that each side makes
with the horizontal by an equal amount.
The director wants the car to be stopped
at the bottom of one side of the bridge
and then accelerate up that side in an
amount of time which will allow for all
the necessary dramatic camera shots. He
wants you to determine the necessary
constant acceleration as a function of
that time, the gap between the two sides
of the open bridge, the angle that the
side of the open bridge makes with the
horizontal, and the mass of the car.
- You have been hired as a technical
consultant for a new action movie. The
director wants a scene in which a car
goes up one side of an open drawbridge,
leaps over the gap between the two sides
of the bridge, and comes down safely on
the other side of the bridge. This
drawbridge opens in the middle by
increasing the angle that each side makes
with the horizontal by an equal amount.
The director wants the car to be stopped
at the bottom of one side of the bridge
and then accelerate up that side in an
amount of time which will allow for all
the necessary dramatic camera shots. He
wants you to determine the necessary
constant acceleration as a function of
that time, the gap between the two sides
of the open bridge, the angle that the
side of the open bridge makes with the
horizontal, and the mass of the car.
The following three problems have a very unfamiliar contexts.
- You are sitting in front of your TV waiting for
the World Series to begin when your mind wanders.
You know that the image on the screen is created
when electrons strike the screen which then gives
off light from that point. In the first TV sets,
the electron beam was moved around the screen to
make a picture by passing the electrons between
two parallel sheets of metal called electrodes.
Before the electrons entered the gap between the
electrodes, which deflect the beam vertically,
the electrons had a velocity of 1.0 x 106 m/s
directly toward the center of the gap and toward
the center of the screen. Each electrode was 5.0
cm long (direction the electron was going), 2.0
cm wide and the two were separated by 0.5 cm. A
voltage was applied to the electrodes which
caused the electrons passing between them to have
a constant acceleration directly toward one of
the electrodes and away from the other. After the
electrons left the gap between the electrodes
they were not accelerated and they continued
until they hit the screen. The screen was 15 cm
from the end of the electrodes. What vertical
electron acceleration between the electrodes
would be necessary to deflect the electron beam
20 cm from the center of the screen? DO ONLY THE
PROBLEM SOLVING STEPS NECESSARY TO FOCUS THE
PROBLEM AND DESCRIBE THE PHYSICS OF THE PROBLEM.
DO NOT SOLVE THIS PROBLEM.
- You have a summer job in the cancer therapy division of
a hospital. This hospital treats cancer by hitting the tumor with high
energy protons from a cyclotron. When the protons leave the cyclotron
they are going at half the speed of light. You are in charge of
deflecting the protons so they hit the patent's tumor. This deflection
is accomplished by passing the proton beam between two flat, parallel
electrodes that have a length of 10 feet in the entering beam direction.
The protons enter the region between the electrodes going parallel to
their surface. The two electrodes are separated by 1.5 inches. A high
voltage is applied to the electrodes so that the protons passing between
them have a constant acceleration as they are attracted directly toward
one and repelled by the other. After the protons leave the region
between the plates, they are no longer accelerated during the remaining
200 feet to the patient. To set the correct high voltage, you need to
calculate the magnitude of the acceleration the protons need when they
are between the plates so that they are deflected by 1.0 degree, the
angle between the incident beam and the beam hitting the patient. The
speed of light is 1.0 foot per nanosecond.
- You have a summer job as an assistant in a
University research group that is designing a
devise to sample atmospheric pollution. In this
devise, it is useful to separate fast moving ions
from slow moving ones. To do this the ions are
brought into the device in a narrow beam so that
all of the ions are going in the same direction.
The ion beam then passes between two parallel
metal plates. Each plate is 5.0 cm long, 4.0 cm
wide and the two plates are separated by 3.0 cm.
A high voltage is applied to the plates causing
the ions passing between them to have a constant
acceleration directly toward one of the plates
and away from the other plate. Before the ions
enter the gap between the plates , they are going
directly toward the center of the gap parallel to
the surface of the plates. After the ions leave
the gap between the plates, they are no longer
accelerated during the 50 cm journey to the ion
detector. Your boss asks you to calculate the
magnitude of acceleration between the plates
necessary to separate ions with a velocity of 100
m/s from those in the beam going 1000 m/s by 2.0
cm?
Note: Each problem begins with a list of forces necessary to solve the context-rich problem. These are for the benefit of the instructor. Delete the list before using the problems in your class.
- Tension, WeightSOLUTION :FOR THE FOLLOWING PLAN
THE PROBLEM. An artist friend of yours wants your opinion
of his idea for a new kinetic sculpture. The basic
concept is to balance a heavy object with two lighter
objects using two very light pulleys, which are
essentially frictionless, and lots of string. The
sculpture has one pulley hanging from the ceiling by a
string attached to its center. Another string passes over
this pulley. One end of this string is attached to a 25
lb object while the other supports another pulley at its
center. This second pulley also has a string passing over
it with one end attached to a 10 lb object and the other
to a 15 lb object. Your friend hasn't quite figured out
the rest of the sculpture but wants to know if, ignoring
the mass of the pulley and string, the 25 lb object will
remain stationary during the time that the 10 and 15 lb
objects are accelerating. DO NOT SOLVE THE PROBLEM.
- Weight, Normal: You have always been impressed by the
speed of the elevators in the IDS building in Minneapolis
(especially compared to the one in the Physics building).
You wonder about the maximum acceleration for these
elevators during normal operation, so you decide to
measure it by using your bathroom scale. While the
elevator is at rest on the ground floor, you get in, put
down your scale, and stand on it. The scale reads 130
lbs. You continue standing on the scale when the elevator
goes up, carefully watching the reading. During the trip
to the 50th floor, the greatest scale reading was 180
lbs.
- You are designing a lamp for the interior of a special
executive express elevator in a new office building. The lamp has two
sections that hang one directly below the other. The bottom section is
attached to the top one by a single thin wire and the upper section is
attached to the ceiling by another single thin wire. Because the idea is
to make each section appear to be floating without support, you want to
use the thinnest (and thus weakest) wire possible. You decide to
calculate the force each wire must exert on the lamp sections in case of
an emergency stop. The elevator has all the latest safety features and
will stop with an acceleration of g/3 in any emergency. Each section of
the lamp weighs 7.0 N.
- You are investigating an elevator accident which happened
in a tall building. An elevator in this building is
attached to a strong cable which runs over a pulley
attached to a steel support in the roof. The other end of
the cable is attached to a block of metal called a
counterweight which hangs freely. An electric motor on
the side of the elevator drives the elevator up or down
by exerting a force on the side of the elevator shaft.
You suspect that when the elevator was fully loaded,
there was too large a force on the motor . A fully loaded
elevator at maximum capacity weighs 2400 lbs. The
counterweight weighs 1000 lbs. The elevator always starts
from rest at its maximum acceleration of g/4 whether it
is going up or down. (a) What force does the wall of the
elevator shaft exert on the motor if the elevator starts
from rest and goes up? (b) What force does the wall of
the elevator shaft exert on the motor if the elevator
starts from rest and goes down?
- Tension, Weight: An artist friend of yours wants your
opinion of his idea for a new kinetic sculpture. The
basic concept is to balance a heavy object with two
lighter objects using two very light pulleys, which are
essentially frictionless, and lots of string. The
sculpture has one pulley hanging from the ceiling by a
string attached to its center. Another string passes over
this pulley. One end of this string is attached to a
25-lb object while the other supports another pulley at
its center. This second pulley also has a string passing
over it with one end attached to a 10-lb object and the
other to a 15-lb object. Your friend hasn't quite figured
out the rest of the sculpture but wants to know if,
ignoring the mass of the pulley and string, the 25-lb
object will remain stationary during the time that the
10-lb and 15-lb objects are accelerating. DO ONLY THE
PROBLEM SOLVING STEPS NECESSARY TO FOCUS THE PROBLEM,
DESCRIBE THE PHYSICS OF THE PROBLEM, AND PLAN A SOLUTION.
DO NOT SOLVE THIS PROBLEM.
- Weight, Normal, Friction: Because of your physics background,
you have been asked to check the feasibility of a action movie stunt. In
the script, the hero and villain are fighting on top of a locomotive
heading down a straight track at 25 mph. Having jumped on the train as
it passed over a lake, the hero is dressed in a rubber wet suit. During
the fight, the hero slips off and barely hangs on over the top edge of
the front of the locomotive, which is essentially a vertical smooth
steel face. The villain stomps on the hero's fingers to cause the hero
to let go and be crushed under the train. Meanwhile, the hero's partner
has been trying to stop the train, whose brakes have been locked by the
villain. Seeing the heroâs fingers give way, the partner immediately
opens the throttle, causing the train to accelerate forward and the hero
to stay on the front face of the locomotive without slipping down until
the brakes can be unlocked. The movie company wants to know what minimum
acceleration is necessary to perform this stunt. The hero weighs 180
lbs. and the locomotive weighs 100 tons. Looking in a book giving the
properties of materials, you find that for rubber on steel, the
coefficient of kinetic friction is 0.50 and the coefficient of static
friction is 0.60.
- Weight, Normal, Friction: While working in a mechanical
structures laboratory, your boss assigns you to test the
strength of ropes under different conditions. Your test
set-up consists of two ropes attached to a 30 kg block
which slides on a 5.0 m long horizontal table top. Two
low friction, light weight pulleys are mounted at
opposite ends of the table. One rope is attached to each
end of the 30 kg block. Each of these ropes runs
horizontally over a different pulley. The other end of
one of the ropes is attached to a 12 kg block which hangs
straight down. The other end of the second rope is
attached to a 20 kg block also hanging straight down. The
coefficient of kinetic friction between the block on the
table and the table's surface is 0.08. The 30 kg block is
initially held in place by a mechanism that is released
when the test begins so, that the block is accelerating
during the test. During this test, what is the force
exerted on the rope supporting the 12 kg block?
- Human, Weight, Normal: You are taking care of two small
children, Sarah and Rachel, who are twins. On a nice
cold, clear day you decide to take them ice skating on
Lake of the Isles. To travel across the frozen lake you
have Sarah hold your hand and Rachel's hand. The three of
you form a straight line as you skate, and the two
children just glide. Sarah must reach up at an angle of
60 degrees to grasp your hand, but she grabs Rachel's
hand horizontally. Since the children are twins, they are
the same height and the same weight, 50 lbs. To get
started you accelerate at 2.0 m/s2. You are concerned
about the force on the children's arms which might cause
shoulder damage. So you calculate the force Sarah exerts
on Rachel's arm, and the force you exert on Sarah's other
arm. You assume that the frictional forces of the ice
surface on the skates are negligible.
- Tension, Weight, Normal, and Friction: You are planning to
build a log cabin and will need to pull the logs up a hill to the
building site by means of a rope attached to a winch. In order to buy
the rope, you need to know how strong the rope must be and decide to do
a quick calculation for this. The logs weigh 500 lbs. at most and the
hill is at an angle of 30° with respect to the horizontal. You estimate
that the coefficient of kinetic friction between a log and the hill is
0.90. When pulling a log up the hill, you will make sure that the rope
stays parallel to the surface of the hill and the acceleration of the
log is never more than 0.80 m/s^2.
- Tension, Weight, Normal, Friction: At your job at a
warehouse, you have designed a method to help get heavy packages up a
15º ramp. The package is attached to a rope that runs parallel to the
ramp and passes over a pulley at the top of the ramp. The other end of
the rope is attached to a counterweight that hangs straight down. The
mass of the counterweight is always adjusted to be twice the mass of the
package. However, your boss is worried that the acceleration of the
package will make it too difficult to handle at the top of the ramp and
tells you to calculate it. To determine the influence of friction on the
package by the ramp, you run some tests and find that using a horizontal
force of 250 Newtons, you can push a 50 kg package at a constant speed
along a level floor made of the same material as the ramp.
- Tension, Weight, Normal, Friction: After graduating you
get a job in Northern California. To move there, you rent
a truck for all of your possessions. You also decide to
take your car with you by towing it behind the truck. The
instructions you get with the truck tells you that the
maximum truck weight when fully loaded is 20,000 lbs and
that the towing hitch that you rented has a maximum
strength of 1000 lbs. Just before you leave, you weigh
the fully loaded truck and find it to be 15,000 lbs. At
the same time you weigh your car and find it to weigh
3000 lbs. You begin to worry if the hitch is strong
enough. Then you remember that you can push your car and
can easily keep it moving at a constant velocity. You
know that air resistance will increase as the car goes
faster but from your experience you estimate that the sum
of the forces due to air resistance and friction on the
car is not more than 300 lbs. If the largest hill you
have to go up is sloped at 10o from the horizontal, what
is the maximum acceleration you can safely have on that
hill? DO ONLY THE PROBLEM SOLVING STEPS NECESSARY TO
FOCUS THE PROBLEM, DESCRIBE THE PHYSICS OF THE PROBLEM,
AND PLAN A SOLUTION. DO NOT SOLVE THIS PROBLEM.
- Weight, Normal, Friction: Because of your physics
background, you have been able to get a job with a
company devising stunts for an upcoming adventure movie
being shot in Minnesota. In the script, the hero has been
fighting the villain on the top of the locomotive of a
train going down a straight horizontal track at 20 mph.
He has just snuck on the train as it passed over a lake
so he is wearing his rubber wet suit. During the fight,
the hero slips and hangs by his fingers on the top edge
of the front of the locomotive. The locomotive has a
smooth steel front face sloped at 20o from the vertical
so that the bottom of the front is more forward that the
top. Now the villain stomps on the hero's fingers so he
will be forced to let go and slip down the front of the
locomotive and be crushed under its wheels. Meanwhile,
the hero's partner is at the controls of the locomotive
trying to stop the train. To add to the suspense, the
brakes have been locked by the villain. It will take her
10 seconds to open the lock. To her horror, she sees the
hero's fingers give way before she can get the lock off.
Since she is the brains of the outfit, she immediately
opens the throttle causing the train to accelerate
forward. This causes the hero to stay on the front face
of the locomotive without slipping down giving her time
to save the hero's life. The movie company wants to know
what minimum acceleration is necessary to perform this
stunt. The hero weighs 180 lbs in his wet suit. The
locomotive weighs 100 tons. You look in a book giving the
properties of materials and find that the coefficient of
kinetic friction for rubber on steel is 0.50 and its
coefficient of static friction is 0.60.
- Gravitational: You have been hired as a consultant for
the new Star Trek TV series to make sure that any science
on the show is correct. In this episode, the crew of the
Enterprise discovers an abandoned space station in deep
space far from any stars. This station is obviously the
work of an advanced race and consists of four identical 3
x 1020 kg asteroids configured so that each is at the
corner of a square with 200 km sides. According to the
tricorder, the station has been abandoned for at least
two centuries. You know that such a configuration is
unstable and worry whether there would be observable
motion of the asteroids after two hundred years so you
calculate the acceleration of one of the asteroids in the
proposed configuration. Make sure you give both the
magnitude and the direction of the acceleration.
- Gravitational: Because the movie industry is trying to
make the technical details of movies as correct as
possible, you have been made a member of a panel
reviewing the details of a new science fiction script.
Although neither astronomy nor navigation is your field,
you are disturbed by one scene in which a space ship
which is low on fuel is attempting to land on the Earth.
As the ship approaches, it is heading straight for the
center of the Earth. The commander cuts off the ship's
engines so that it will be pulled in by the Earth's
gravitational force. As the commander looks in the
viewer, she sees the Earth straight ahead and the Moon
off to the left at an angle of 30o. The line between the
centers of the Moon and Earth is at right angles to the
initial path of the space ship. Under these conditions
you don't think the ship will continue heading toward the
Earth, so you calculate the component of its acceleration
which is perpendicular to the initial path of the ship.
First you look up the distance between the Earth and the
Moon (3.8 x 105 km), the mass of the Earth (6.0 x 1024
kg), the mass of the Moon (7.3 x 1022 kg), the radius of
the Earth (6.4 x 103 km), the radius of the Moon (1.7 x
103 km), and the universal gravitational constant (6.7 x
10-11 N m2/kg2). As a first approximation, you decide to
neglect the effect of the Sun and the other planets in
the solar system. You guess that a space ship such as
described in the script might have a mass of about
100,000 kg.
- Weight - Buoyancy, Normal, Friction, Electric: The
quarter is almost over so you decide to have a party. To
add atmosphere to your otherwise drab apartment, you
decide to decorate with balloons. You buy about fifty and
blow them up so that they are all sitting on your carpet.
After putting most of them up, you decide to play with
the few balloons left on the floor. You rub one on your
sweater and find that it will "stick" to a
wall. Ah ha, you know immediately that you are observing
the electric force in action. Since it will be some time
before you guests arrive and you have already made the
onion dip, you decide to calculate the minimum electric
force of the wall on the balloon. You know that the air
exerts a net upward force (the "buoyant" force)
on the balloon which makes it almost float. You measure
that the weight of the balloon minus the buoyant force of
the air on the balloon is 0.05 lb. By reading your
physics book, you estimate that the coefficient of static
friction between the wall and the balloon (rubber and
concrete) is 0.80.
- Tension, Weight, Electric: While working in a
University research laboratory you are given the job of
testing a new device for precisely measuring the weight
of small objects. The device consists of two very light
strings attached at one end to a support. An object is
attached to the other end of each string. The strings are
far enough apart so that objects hanging on them don't
touch. One of the objects has a very accurately known
weight while the other object is the unknown. A power
supply is slowly turned on to give each object an
electric charge which causes the objects to slowly move
away from each other (repel) because of the electric
force. When the power supply is kept at its operating
value, the objects come to rest at the same horizontal
level. At that point, each of the strings supporting them
makes a different angle with the vertical and that angle
is measured. To test the device, you want to calculate
the weight of an unknown sphere from the measured angles
and the weight of a known sphere. You use a standard
sphere with a known weight of 2.000 N supported by a
string which makes an angle of 10.0º with the vertical.
The unknown sphere's string makes an angle of 20.0º with
the vertical.
- Gravitational: You are writing a short science fiction
story for your English class. You get your idea from the
fact that when people cross the Earth's equator for the
first time, they are awarded a certificate to commemorate
the experience. In your story it is the 21st Century and
you are the tour director for a trip to the moon.
Transplanetary Tours promises tour participants a
certificate to commemorate their passage from the
stronger influence of the Earth's gravitational pull to
the stronger gravitational pull of the moon. To finish
the story, you need to figure out where on the trip you
should award the certificate. In your physics book you
look up the distance between the Earth and the Moon (3.8
x 105 km), the mass of the Earth (6.0 x 1024 kg), the
mass of the Moon (7.3 x 1022 kg), the radius of the Earth
(6.4 x 103 km), the radius of the Moon (1.7 x 103 km),
and the universal gravitational constant (6.7 x 10-11 N
m2/kg2).
- Gravitational: You have been hired as a consultant for
the new Star Trek TV series to make sure that the science
in the show is correct. In this episode, the crew of the
Enterprise goes into standard orbit around a newly
discovered planet. The plot requires that the planet is
hollow and contains the underground cities of a lost
civilization. From orbit the science officer determines
that the radius of the planer is 1/4 (one-fourth) that of
Earth. The first officer beams down to the surface of the
planet and measures that his weight is only 1/2
(one-half) of his weight on Earth. How does the mass of
this planet compare with the mass of the Earth? If it
were hollow, its density would be less than Earth. Are
the measurements consistent with a hollow planet?
- Gravitational, Electric: You and a friend are reading a
newspaper article about nuclear fusion energy generation
in stars. The article describes the helium nucleus, made
up of two protons and two neutrons, as very stable so it
doesn't decay. You immediately realize that you don't
understand why the helium nucleus is stable. You know
that the proton has the same charge as the electron
except that the proton charge is positive. Neutrons you
know are neutral. Why, you ask your friend, don't the
protons simply repel each other causing the helium
nucleus to fly apart? Your friend says she knows why the
helium nucleus does not just fly apart. The gravitational
force keeps it together, she says. Her model is that the
two neutrons sit in the center of the nucleus and
gravitationally attract the two protons. Since the
protons have the same charge, they are always as far
apart as possible on opposite sides of the neutrons. What
mass would the neutron have if this model of the helium
nucleus works? Is that a reasonable mass? Looking in your
physics book, you find that the mass of a neutron is
about the same as the mass of a proton and that the
diameter of a helium nucleus is 3.0 x 10-13 cm.
- Tension, Weight, Friction: You are taking
advantage of an early snow to go sledding. After a long
afternoon of going up and down hills with your sled, you
decide it is time to go home. You are thankful that you
can pull your sled without climbing any more hills. As
you are walking home, dragging the sled behind you by a
rope fastened to the front of the sled, you wonder what
the coefficient of friction of the snow on the sled is.
You estimate that you are pulling on the rope with a 2
pound force, that the sled weighs 10 pounds, and that the
rope makes an angle of 25 degrees to the level ground.
- Human, Weight, Normal, Friction: You are helping a friend
move into a new apartment. A box weighing 150 lbs needs
to be moved to make room for a couch.. You are taller
than the box, so you reach down to push it at an angle of
50 degrees from the horizontal. The coefficient of static
friction between the box and the floor is 0.50 and the
coefficient of kinetic friction between the box and the
floor is 0.30. (a) If you want to exert the minimum force
necessary, how hard would you push to keep the box moving
across the floor? (b) Suppose you bent your knees so that
your push were horizontal. How hard would you push to
keep the box moving across the floor?
- Human, Weight, Normal, Friction: You are helping an
investigation of back injuries in the construction
industry. Your assignment is to determine why there is a
correlation of the height of the worker to the likelihood
of back injury. You suspect that some back injuries are
related to the way people push heavy objects in order to
move them. When people push an object, such as a box,
across the floor they tend to lean down and push at an
angle to the horizontal. Taller people push at a larger
angle with respect to the horizontal than shorter people.
To present your ideas to the rest of the research team,
you decide to calculate the force a 200-lb box exerts on
a 150-lb person when they push it across a typical floor
at a constant velocity of 7.0 ft/s as a function of the
angle with respect to the horizontal at which the person
pushes the box. Once you have your function, you will use
angles of 0o, 10o, 20o, 30o, and 40o to make a graph of
the result for the presentation. One of your coworkers
tells you that a typical coefficient of static friction
between a box and a floor of 0.60 and while a typical
coefficient of kinetic friction between a box and a floor
is 0.50. (Don't forget to make the graph).
- Tension, Weight: Your are part of a team to help design
the atrium of a new building. Your boss, the manager of
the project, wants to suspend a 20-lb sculpture high over
the room by hanging it from the ceiling using thin, clear
fishing line (string) so that it will be difficult to see
how the sculpture is held up. The only place to fasten
the fishing line is to a wooden beam which runs around
the edge of the room at the ceiling. The fishing line
that she wants to use will hold 20 lbs (20-lb test) so
she suggests attaching two lines to the sculpture to be
safe. Each line would come from the opposite side of the
ceiling to attach to the hanging sculpture. Her initial
design has one line making an angle of 20o with the
ceiling and the other line making an angle of 40o with
the ceiling. She knows you took physics, so she asks you
if her design can work.
- Electric, Weight, Tension: While working in a University research laboratory you are given the job of testing a new device, called an electrostatic scale, for precisely measuring the weight of small objects. The device is quite simple. It consists of two very light but strong strings attached to a support so that they hang straight down. An object is attached to the other end of each string. One of the objects has a very accurately known weight while the other object is the unknown. A power supply is slowly turned on to give each object an electric charge which causes the objects to slowly move away from each other (repel) because of the electric force. When the power supply is kept at its operating value, the objects come to rest at the same horizontal level. At that point, each of the strings supporting them makes a different angle with the vertical and that angle is measured. To test the device, you want to calculate the weight of an unknown sphere from the measured angles and the weight of a known sphere. You use a standard sphere with a known weight of 2.00000 N supported by a string which makes an angle of 10.00o with the vertical. The unknown sphere's string makes an angle of 20.00o with the vertical.
Note: Each problem begins with a list of forces necessary to solve the context-rich problem. These are for the benefit of the instructor. Delete the list before using the problems in your class.
- Weight, Normal: While driving in the mountains, you
notice that when the freeway goes steeply down hill,
there are emergency exits every few miles. These
emergency exits are straight dirt ramps which leave the
freeway and are sloped uphill. They are designed to stop
trucks and cars that lose their breaks on the downhill
stretches of the freeway even if the road is covered in
ice. You are curious, so you stop at the next emergency
road. You estimate that the road rises at an angle of 10o
from the horizontal and is about 100 yards (300 ft) long.
What is the maximum speed of a truck that you are sure
will be stopped by this road, even if the frictional
force of the road surface is negligible?
- Weight, Normal: While driving in the mountains, you
notice that when the freeway goes steeply down hill,
there are emergency exits every few miles. These
emergency exits are straight dirt ramps which leave the
freeway and are sloped uphill. They are designed to stop
trucks and cars that lose their breaks on the downhill
stretches of the freeway even if the road is covered in
ice. You wonder at what angle from the horizontal an
emergency exit should rise to stop a 50 ton truck going
70 mph up a ramp 100 yards (300 ft) long, even if the
frictional force of the road surface is negligible.
- Weight, Normal: You have opened a small delivery business that
guarantees to deliver any box between 5 lbs. and 500 lbs. to any
location in the area by the next day. At your distribution center, boxes
slide down a ramp between the delivery and the sorting area. You must
determine the angle this ramp should have so that a box will take 5.0
seconds to slide down the ramp when starting from rest at the top. When
the box arrives at the bottom of the ramp, you decide that its speed
should be no larger than 10 ft/s so as not to damage the contents of the
box. Using the latest technology, the surface of the ramp will be
extremely slippery.
- Weight, Normal: You are watching a ski jump contest on
television when you wonder how high the skier is when she
leaves the starting gate. In the ski jump, the skier
glides down a long ramp. At the end of the ramp, the
skier glides along a short horizontal section which ends
abruptly so that the skier goes into the air. You
measured that the skier was in the air for 2.3 seconds
and landed 87 meters, in the horizontal direction, from
the point she went into the air. Make the best estimate
of the height of the starting gate at the top of the ramp
from the horizontal section from which the skier takes
off into the air. Make clear on what assumptions your
answer depends (this is why it is an estimate).
- Weight, Normal, Friction: You are passing a construction
site on the way to physics class, and stop to watch for
awhile. The construction workers appear to be going on
coffee break, and have left a large concrete block
resting at the top of a wooden ramp. As soon as their
backs are turned, the block begins to slide down the
ramp. You quickly clock the time for the block to reach
the bottom of the ramp at 10 seconds. You wonder how long
the ramp is. You estimate that the ramp is at an angle of
about 20o to the horizontal. In your physics book you
find that the coefficient of kinetic friction between
concrete and wood is 0.35.
- Weight, Normal, Friction: You have a summer job at a
company that specializes in the design of sports
facilities. The company has been given the contract to
design a new hockey rink to try to keep the North Stars
in town. The rink floor is very flat and horizontal and
covered with a thick coat of ice. Your task is to
determine the refrigeration requirements which gives best
temperature for the ice. You have a table which gives the
coefficient of static and kinetic friction between ice
and the standard NHL hockey puck as a function of ice
temperature. You have been told that the hockey game will
be more exciting if passes are swift and sure. Experts
say that the passing game is best if, after it goes 5.0
m, a puck has a speed which is 90% of the speed with
which it left the hockey stick. A puck typically has a
speed of 20 km/hr when it leaves the hockey stick for a
pass.
- Weight, Normal, Friction: You and some friends visit the
Minnesota State Fair and decide to play a game on the
Midway. To play the game you must slide a metal
hockey-type puck up a wooden ramp so that it drops
through a hole at the top of the ramp. Your prize, if you
win, is a large, pink, and rather gaudy, stuffed poodle.
You realize the secret to winning is giving the puck just
enough velocity at the bottom of the ramp to make it to
the hole. You estimate the distance from the bottom of
the ramp to the hole at about 10 feet, and the ramp
appears to be inclined with an angle of 10o from the
horizontal. You just got out of physics class and recall
the coefficient of static friction between steel and wood
is 0.1 and the coefficient of kinetic friction between
steel and wood is 0.08. The mass of the puck is about 2.5
lbs. You decide to impress your friends by sliding the
puck at the precise speed on the first try so as to land
it in the hole. You slide the puck at 8.0 ft/sec. Do you
win the stuffed poodle?
- Weight, Normal, Tension, Friction: Finally you are
leaving Minneapolis to get a few days of Spring break,
but your car breaks down in the middle of nowhere. A tow
truck weighing 4000 lbs comes along and agrees to tow
your car, which weighs 2000 lbs, to the nearest town. The
driver of the truck attaches his cable to your car at an
angle of 20o to the horizontal. He tells you that his
cable has a strength of 500 lbs. He plans to take 10
seconds to tow your car at a constant acceleration from
rest in a straight line along the flat road until he
reaches the maximum speed limit of 45 miles/hour. Can the
driver carry out his plan? You assume that rolling
friction behaves like kinetic friction, and the
coefficient of rolling friction between your tires and
the road is 0.10.
- Weight, Normal, Friction: While visiting a friend in San
Francisco you decide to drive around the city. You turn a
corner and are driving up a steep hill. Suddenly, a small
boy runs out on the street chasing a ball. You slam on
the brakes and skid to a stop leaving a 50 foot long skid
mark on the street. The boy calmly walks away but a
policeman watching from the sidewalk walks over and gives
you a ticket for speeding. You are still shaking from the
experience when he points out that the speed limit on
this street is 25 mph. After you recover your wits, you
examine the situation more closely. You determine that
the street makes an angle of 20o with the horizontal and
that the coefficient of static friction between your
tires and the street is 0.80. You also find that the
coefficient of kinetic friction between your tires and
the street is 0.60. Your car's information book tells you
that the mass of your car is 1570 kg. You weigh 130 lbs.
Witnesses say that the boy had a weight of about 60 lbs
and took 3.0 seconds to cross the 15 foot wide street.
Will you fight the ticket in court?
- Weight, Lift, Thrust, Drag: One morning while waiting for class to begin, you are reading a newspaper article about airplane safety. This article emphasizes the role of metal fatigue in recent accidents. Metal fatigue results from the flexing of airframe parts in response to the forces on the plane especially during take off and landings. As an example, the reporter uses a plane with a take off weight of 200,000 lbs and take off speed of 200 mph which climbs at an angle of 30o with a constant acceleration to reach its cruising altitude of 30,000 feet with a speed of 500 mph. The three jet engines provide a forward thrust of 240,000 lbs by pushing air backwards. The article then goes on to explain that a plane can fly because the air exerts an upward force on the wings perpendicular to their surface called "lift." You know that air resistance is also a very important force on a plane and is in the direction opposite to the velocity of the plane. The article tells you this force is called the "drag." Although the reporter writes that some metal fatigue is primarily caused by the lift and some by the drag, she never tells you their size for her example plane. Luckily the article contains enough information to calculate them, so you do.
Note: Each problem begins with a list of forces necessary to solve the context-rich problem. These are for the benefit of the instructor. Delete the list before using the problems in your class.
- Weight, Normal: Just before finals you decide to visit an
amusement park set up in the Metrodome. Since it is a
weekend, you invite your favorite niece along. She loves
to ride on a Ferris wheel, and there is one at the
amusement park. The Ferris wheel has seats on the rim of
a circle with a radius of 25 m. The Ferris wheel rotates
at a constant speed and makes one complete revolution
every 20 seconds. While you wait, your niece who has a
mass of 42 kg, rides the Ferris wheel. To kill time you
decide to calculate the total force (both magnitude and
direction) on her when she is one quarter revolution past
the highest point. Because the Ferris wheel can be run at
different speeds, you also decide to make a graph which
gives the magnitude of the force on her at that point as
a function of the period of the Ferris wheel.
- Weight, Normal: While watching TV, you see a circus show
in which a performer drives a motorcycle around the inside of a vertical
ring. You wonder how far the cycle would fall if the rider made a
mistake at the top of the loop and fell off the track and decide to
calculate it. You determine that the cycle is going around at a constant
speed and that it takes at most 4.0 seconds to get around the ring. At
this speed, the motorcycle just barely loses contact with the ring at
the top when it is upside down and is in free fall.
- Weight, Normal, Friction: The producer of the last film
you worked on was so impressed with the way you handled a
helicopter scene that she hired you again as technical
advisor for a new "James Bond" film. The scene
calls for 007 to chase a villain onto a merry-go-round.
An accomplice starts the merry-go-round rotating in an
effort to toss 007 (played in this new version by Billy
Crystal) off into an adjacent pool filled with hungry
sharks. You must determine a safe rate of rotation such
that the stunt man (you didn't think Billy would do his
own stunts did you?) will not fly off the merry-go-round
and into the shark-infested pool. (Actually they are
mechanical sharks, but the audience doesn't know that.)
You measure the diameter of the merry-go-round as 50
meters. You determine that the coefficient of static
friction between 007's shoes and the merry-go-round
surface is 0.7 and the coefficient of kinetic friction is
0.5.
- Weight, Normal, Friction: A new package moving
system in the new, improved post office consists of a
large circular disc (i.e. a turntable) which rotates once
every 3.0 seconds at a constant speed in the horizontal
plane. Packages are put on the outer edge of the
turntable on one side of the room and taken off on the
opposite side. The coefficient of static friction between
the disc surface and a package is 0.80 while the
coefficient of kinetic friction is 0.60. If this system
is to work, what is the maximum possible radius of the
turntable?
- Weight, Normal, Friction: You are driving with a friend
who is sitting to your right on the passenger side of the
front seat. You would like to be closer to your friend
and decide to use your knowledge of physics to achieve
your romantic goal. So you'll make a sharp turn. Which
direction should you turn so as to make your friend slide
closer to you? If the coefficient of static friction
between your friend and the seat of the car is 0.40, and
you drive at a constant speed of 18 m/s, what is the
maximum radius you could make your turn and still have
your friend slide your way?
- Weight, Normal, Friction: During a freeway safety review, you
are studying a piece of one road with a curve that is essentially 1/8 of
a circle with a radius of 0.5 miles. The curve is banked so that the
road makes an angle of 4 degrees to the horizontal throughout the curve.
Your boss asks you to help determine the speed limit for a standard
passenger car (about 2000 lbs) to complete the turn. You decide to start
by considering the worst-case scenario, a slick, ice-covered road, and
finding the constant speed a car must travel in order to maintain a
horizontal path through the turn.
- Weight, Tension: After watching the movie "Crocodile
Dundee," you and some friends decide to make a
communications device invented by the Australian
Aborigines. It consists of a noise-maker swung in a
vertical circle on the end of a string. Your design calls
for a 400 gram noise-maker on a 60 cm string. You are
worried about whether the string you have will be strong
enough, so you decide to calculate the tension in the
string when the device is swung with an acceleration
which has a constant magnitude of 20 m/s2 . You and your
friends can't agree whether the maximum tension will
occur when the noise maker is at the highest point in the
circle, at the lowest point in the circle, or is always
the same. To settle the argument you decide to calculate
the tension at the highest point and at the lowest point
and compare them.
- You are watching a TV news program when they switch to
some scenes taken aboard the space shuttle which circles
500 miles above the Earth once every 95 minutes. To allow
the audience to appreciate the distances involved, the
announcer tells you that the radius of the Earth is about
4000 miles and the distance from the Earth to the Moon is
about 250,000 miles. When an astronaut drops her pen it
floats in front of her face. You immediately wonder how
the acceleration of the dropped pen compares to the
acceleration of a pen that you might drop here on the
surface of the Earth.
- Gravitational: You are still a consultant for the new
Star Trek TV series. You were hired to make sure that any
science on the show is correct. In this episode, the crew
of the Enterprise discovers an abandoned space station in
deep space far from any stars. This station, which was
built by Earth in the 21st century, is a large wheel-like
structure where people live and work in the rim. In order
to create "artificial gravity," the space
station rotates on its axis. The special effects
department wants to know at what rate a space station 200
meters in diameter would have to rotate to create
"gravity" equal to 0.7 that of Earth.
- Gravitational: You did so well in your physics course
that you decided to try to get a summer job working in a
physics laboratory at the University. You got the job as
a student lab assistant in a research group investigating
the ozone depletion at the Earth's poles. This group is
planning to put an atmospheric measuring device in a
satellite which will pass over both poles. To collect
samples of the upper atmosphere, the satellite will be in
a circular orbit 200 miles above the surface of the
Earth. To adjust the instruments for the proper data
taking rate, you need to calculate how many times per day
the device will sample the atmosphere over the South
pole. Using the inside cover of your trusty Physics text
you find that the radius of the Earth is 6.38 x 103 km,
the mass of the Earth is 5.98 x 1024 kg, and the
universal gravitational constant is 6.7 x 10-11 N m2/kg2.
- Gravitational: You did so well in your physics course
that you decided to try to get a summer job working in a
physics laboratory at the University. You got the job as
a student lab assistant in a research group investigating
the ozone depletion at the Earth's poles. This group is
planning to put an atmospheric measuring device in a
satellite which will pass over both poles. To collect
samples of the upper atmosphere, the satellite will be in
a circular orbit 200 miles above the surface of the Earth
where g is 95% of its value on the Earth's surface. To
adjust the instruments for the proper data taking rate,
you need to calculate how many times per day the device
will sample the atmosphere over the South pole. Using the
inside cover of your trusty Physics text you find that
the radius of the Earth is 6.38 x 103 km and the mass of
the Earth is 5.98 x 1024 kg.
- Gravitational: You are reading a magazine article about
pulsars. A few years ago, a satellite in orbit around the
Earth detected X-rays coming from sources in outer space.
The X-rays detected from one source, called Cygnus X-3,
had an intensity which changed with a period of 4.8
hours. This type of astronomical object emitting periodic
signals is called a pulsar. One popular theory holds that
the pulsar is a normal star (similar to our Sun) which is
in orbit around a much more massive neutron star. The
period of the X-ray signal is then the period of the
orbit. In this theory, the distance between the normal
star and the neutron star is approximately the same as
the distance between the Earth and our Sun. You realize
that if this theory is correct, you can determine how
much more massive the neutron star is than our Sun. All
you need to do is first find the mass of the neutron star
in terms of two unknowns, the universal gravitational
constant G and the radius of the Earth's orbit. Then find
the mass of our Sun in terms of the same two unknowns, G
and the radius of the Earth's orbit. (The period of the
Earth's orbit is 1 year). Then you can calculate how many
times more massive the neutron star is than our Sun.
- Weight, Lift: You are reading an article about the
aesthetics of airplane design. One example in the article
is a beautiful new design for commercial airliners. You
are worried that this light wing structure might not be
strong enough to be safe. The article explains that an
airplane can fly because the air exerts a force, called
"lift," on the wings such that the lift is
always perpendicular to the wing surface. For level
flying, the wings are horizontal. To turn , the pilot
"banks" the plane so that the wings are
oriented at an angle to the horizontal. This causes the
plane to have a trajectory which is a horizontal circle.
The specifications of the 100 x 103 lb plane require that
it be able to turn with a radius of 2.0 miles at a
constant speed of 500 miles/hr. The article states that
tests show that the new wing structure will support a
force 4 times the lift necessary for level flight. Is the
wing structure sufficiently strong for the plane to make
this turn?
- Weight, Lift: You are flying to Chicago when the pilot
tells you that the plane can not land immediately because
of airport delays and will have to circle the airport.
This is standard operating procedure. She also tells you
that the plane will maintain a speed of 400 mph at an
altitude of 20,000 feet while traveling in a horizontal
circle around the airport. To pass the time you decide to
figure out how far you are from the airport. You notice
that to circle, the pilot "banks" the plane so
that the wings are oriented at 10o to the horizontal. An
article in your in-flight magazine explains that an
airplane can fly because the air exerts a force, called
"lift," on the wings. The lift is always
perpendicular to the wing surface. The magazine article
gives the weight of the type of plane you are on as 100 x
103 pounds and the length of each wing as 150 feet. It
gives no information on the thrust of the engines or the
drag of the airframe.
- Because of your physics background, you have been hired
as a member of the team the state highway department has
assigned to review the safety of Minnesota freeways. This
week you are studying 35W which has a curve which is
essentially 1/8 of a circle with a radius of 0.5 miles.
The road has been designed with a banked curve so that
the road makes an angle of 4û to the horizontal
throughout the curve. To begin the study, the head of
your department asks that you calculate the maximum speed
for a standard passenger car (about 2000 lbs) to complete
the turn while maintaining a horizontal path along the
road. She asks that you first consider the case of a
slick, ice covered road. When you have completed that
calculation she wants you to do the case of a dry, clear
road where the coefficient of kinetic friction is 0.70
and the coefficient of static friction is 0.80 between
the tires and the road. This will give her team the two
extremes of Minnesota driving conditions on which to base
the analysis.
- Tension, Weight: A neighbor's child wants to go to a neighborhood carnival to experience the wild rides. The neighbor is worried about safety because one of the rides looks dangerous. She knows that you have taken physics and so asks your advice. The ride in question has a 10-lb chair which hangs freely from a 30-ft long chain attached to a pivot on the top of a tall tower. When a child enters the ride, the chain is hanging straight down. The child is then attached to the chair with a seat belt and shoulder harness. When the ride starts up the chain rotates about the tower. Soon the chain reaches its maximum speed and remains rotating at that speed. It rotates about the tower once every 3.0 seconds. When you ask the operator, he says that the ride is perfectly safe. He demonstrates this by sitting in the stationary chair. The chain creaks but holds and he weighs 200 lbs. Has the operator shown that this ride safe for a 50-lb child?
- You are watching a National Geographic Special on
television. One segment of the program is about archer
fish, which inhabit streams in southeast Asia. This fish
actually "shoots" water at insects to knock
them into the water so it can eat them. The commentator
states that the archer fish keeps its mouth at the
surface of the stream and squirts a jet of water from its
mouth at 13 feet/second. You watch an archer fish shoot a
juicy moth off a leaf into the water. You estimate that
the leaf was about 2.5 feet above a stream. You wonder at
what minimum angle from the horizontal the water can be
ejected from the fish's mouth to hit the moth. Since you
have time during the commercial, you quickly calculate
this angle.
- Your artist friend is designing a kinetic sculpture and
asks for your help since she knows that you have had
physics. Part of her sculpture consists of a 6.0-kg
object (you can't tell what it is supposed to be, but
it's art) and a 4.0-kg object which hang straight down
from opposite ends of a very thin, flexible wire. This
wire passes over a smooth, cylindrical, horizontal,
stainless steel pipe 3.0 meters above the floor. The
frictional force between the rod and the wire is
negligible. The 6.0-kg object is held 2.0 meters above
the floor and the other object hangs 0.50 meters above
the floor. When the mechanism releases the 6.0-kg object,
both objects accelerate and one will eventually hit the
floor -- but they don't hit each other. To determine if
the floor will be damaged, calculate the speed of the
object which hits the floor.
- You are driving your car uphill along a straight road.
Suddenly, you see a car run a red light and enter the
intersection just ahead of you. You slam on your brakes
and skid in a straight line to a stop, leaving skid marks
100 feet long. A policeman observes the whole incident
and gives a ticket to the other car for running a red
light. He also gives you a ticket for exceeding the speed
limit of 30 mph. When you get home, you read your physics
book and estimate that the coefficient of kinetic
friction between your tires and the road was 0.60, and
the coefficient of static friction was 0.80. You estimate
that the hill made an angle of about 10owith the
horizontal. You look in your owner's manual and find that
your car weighs 2,050 lbs. Will you fight the traffic
ticket in court?
- You have landed a summer job with a company that has been
given the contract to design the ski jump for the next
Winter Olympics. The track is coated with snow and has an
angle of 25o from the horizontal. A skier zips down the
ski jump ramp so that he leaves it at high speed. The
winner is the person who jumps the farthest after leaving
the end of the ramp. Your task is to determine the height
of the starting gate above the end of the ramp, which
will determine the mechanical structure of the ski jump
facility. You have been told that the typical ski-jumper
pushes off from the starting gate at a speed of 2.0 m/s.
For safety reasons, your design should be such that for a
perfect run down the ramp, the skier's speed before
leaving the end of the ramp and sailing through the air
should be no more than 80 km/hr. You run some experiments
on various skies used by the jumpers and determine that
the coefficient of static friction between the snow and
the skis is 0.10 and its coefficient of kinetic friction
is 0.02. Since the ski-jumpers bend over and wear very
aerodynamic suits, you decide to neglect the air
resistance to make your design.
- The Navy wants a new airplane launcher for their aircraft
carriers that is basically a large spring and your job is to determine
the necessary spring constant. The launcher pushes the plane for a short
distance along a much longer runway. During that same time, the plane's
jet engines supply a constant thrust force for the entire length of the
runway. The planes need to have a minimum velocity by the time they
reach the end of the runway in order to take off successfully.
- You have been hired to design a safety system to protect
drivers going down hills during an ice storm. The planned
system consists of a bumper, which can be considered a
stiff spring, at the bottom of the hill. In the scenario
you are given, the car starts from rest at the top of a
hill which makes an angle q with the horizontal. The
distance that the car slides from the top of the hill
until it is stopped by the spring is L. For the worst
case scenario, assume that there is no frictional force
between the car and road due to the ice. If the maximum
compression of the spring from its equilibrium position
is D, your job is to calculate the required spring
constant k in terms of D, L and q.
- You work for the National Park Service testing a small cannon
used to prevent avalanches by shooting down snow overhanging the sides
of mountains. In order to determine the range of the cannon, it is
necessary to know the speed with which the projectile leaves the cannon
(muzzle speed), relative to the ground. The cannon you are testing has
a weight of 500 lbs. and shoots a 20-lb. projectile. During lab tests
where the cannon is held and cannot move, the muzzle speed is 400 m/s.
You want to calculate the projectile's muzzle speed with respect to the
ground under field conditions when the cannon is mounted so that it is
free to move (recoil) when fired. You take the case where the cannon is
fired horizontally using the same shells as in the laboratory.
- Super Dave has just returned from the hospital where he
spent a week convalescing from injuries incurred when he
was "shot" out of a cannon to land in an airbag
which was too thin. Undaunted, he decides to celebrate
his return with a new stunt. He intends to jump off a
100-foot tall tower with an elastic cord tied to one
ankle, and the other end tied to the top of the tower.
This cord is very light but very strong and stretches so
that it can stop him without pulling his leg off. Such a
cord exerts a force with the same mathematical form as
the spring force. He wants it to be 75 feet long so that
he will be in free fall for 75 feet before the cord
begins to stretch. To minimize the force that the cord
exerts on his leg, he wants it to stretch as far as
possible. You have been assigned to purchase the cord for
the stunt and must determine the elastic force constant
which characterizes the cord that you should order.
Before the calculation, you carefully measure Dave's
height to be 6.0 ft and his weight to be 170 lbs. For
maximum dramatic effect, his jump will be off a diving
board at the top of the tower. From tests you have made,
you determine that his maximum speed coming off the
diving board is 10 ft/sec. Neglect air resistance in your
calculation -- let Dave worry about that.
- As part of a fundraiser, you want the new dean to bungee jump
from a crane. The jump will be made from 44 m above a 2.5 m deep pool of
Jello. A 30 m long bungee cord would be attached to the dean's ankle.
You must convince the dean that your plan is safe for a person of his
mass, 70 kg. As the bungee cord stretches, it will exert a force with
the same properties as the force exerted by a spring. Your plan has the
dean stepping off a platform and being in free fall for the 30 m before
the cord begins to stretch. You must determine the elastic constant of
the bungee cord so that it stretches only 12 m, which will keep the
dean's head just out of the Jello.
- Your artist friend's new work is a simple, high-impact kinetic
sculpture called 'Destruction.' A 200-kg steel block is hung from the
ceiling by an 8-foot-long rope. A second rope is attached to the side
of the block. The other end of this second rope is attached to a motor
which is cleverly mounted so that the rope always pulls the block
horizontally with a constant force. The block starts from rest, hanging
straight down, and is pulled slowly by the motor until it is hanging at
an angle of 30 degrees from the vertical. The horizontal rope is then released
and the block swings and crashes into a wall. Your friend knows you
have taken physics and asks you the minimum energy that the motor must
supply. You perform a test and determine that the block is in
equilibrium when it has been pulled so that it hangs at 30 degrees from
the vertical.
- (Gravitational Energy) Because of your knowledge of
physics and interest in the environment, you have gotten
a summer job with an organization which wants to orbit a
satellite to monitor the amount of chlorine ions in the
upper atmosphere over North America. It has been
determined that the satellite should collect samples at a
height of 100 miles above the Earth's surface.
Unfortunately, at that height air resistance would make
the amount of time the satellite would stay in orbit too
short to be useful. You suggest that an elliptical orbit
would allow the satellite to be close to the Earth over
North America, where data was desired, but farther from
the Earth, and thus out of almost all of the atmosphere,
on the other side of our planet. Your colleague estimates
that the satellite would be traveling at 10,000
miles/hour when it was farthest from the Earth at a
height of 1,000 miles. How fast would the satellite be
traveling when it took its air samples if you neglect air
friction?
- At the train station, you notice a large horizontal spring at
the end of the track where the train comes in. This is a safety device
to stop the train so that it will not plow through the station if the
engineer misjudges the stopping distance. While waiting, you wonder what
would be the fastest train that the spring could stop at its full
compression, 3.0 ft. To keep the passengers safe when the train stops,
you assume a maximum stopping acceleration of g/2. You also guess that a
train weighs half a million lbs. For purpose of getting an estimate, you
decide to assume that all frictional force are negligible.
- Your company is designing an apparatus for an ice skating show.
An ice skater will start from rest and slide down an ice-covered ramp.
At the bottom of the ramp, the skater will glide around an ice-covered
loop which is the inside of a vertical circle before emerging out onto
the skating rink floor. For a spectacular effect, the circular loop will
have a diameter of 30 feet. Your task is to determine the minimum height
from the rink floor to the top of the ramp for the skater to make it
around the loop. When barely making it around, the skater briefly loses
contact with the ice at the top of the loop and at that point the skater
is in free fall.
- In a weak moment you have volunteered to be a human
cannonball at an amateur charity circus. The
"cannon" is actually a 3-foot diameter tube
with a big stiff spring inside which is attached to the
bottom of the tube. A small seat is attached to the free
end of the spring. The ringmaster, one of your soon to be
ex-friends, gives you your instructions. He tells you
that just before you enter the mouth of the cannon, a
motor will compress the spring to 1/10 its normal length
and hold it in that position. You are to gracefully crawl
in the tube and sit calmly in the seat without holding on
to anything. The cannon will then be raised to an angle
such that your speed through the air at your highest
point is 10 ft/sec. When the spring is released, neither
the spring nor the chair will touch the sides of the
12-foot long tube. After the drum roll, the spring is
released and you will fly through the air with the
appropriate sound effects and smoke. With the perfect aim
of your gun crew, you will fly through the air over a
15-foot wall and land safely in the net. You are just a
bit worried and decide to calculate how high above your
starting position you will be at your highest point.
Before the rehearsal, the cannon is taken apart for
maintenance. You see the spring, which is now removed
from the cannon, is hanging straight down with one end
attached to the ceiling. You determine that it is 10 feet
long. When you hang on its free end without touching the
ground, it stretches by 2.0 ft. Is it possible for you to
make it over the wall?
- You are on a committee investigating injuries to students
participating in sports, starting with the high incidence of ankle
injuries on the basketball team. Observing the team practice jump shots
inspires you to try a small calculation. A 50-kg student jumps 1.0 meter
straight up and shoots the 0.80-kg basketball at the top of the jump.
From the path of the basketball, you estimate that the ball left the
hand at 30 degrees from the horizontal at 5 m/s. To determine the horizontal
forces on the ankle, you decide to calculate the student's horizontal
velocity when hitting the ground.
- Because of your interest in the environment and your physics
experience, you have been asked by the Campus Museum of Natural History
to assist in the production of an animated film about hawks. In the
script, a 1.5-kg hawk hovers motionless with respect to the ground when
it sees a goose flying below it. The hawk dives straight down. It
strikes the goose at a speed of 60 km/hr and digs its claws into the
goose's body. The 2.5 kg goose was flying north at 30 km/hr just before
it was struck by the hawk and killed instantly. The animators want to
know the velocity of the hawk and dead goose just after the strike.
- As part of an interview for a summer job with the Coast Guard,
you are asked to help determine the search area for two sunken ships by
calculating their velocity just after they collided. According to the
last radio transmission from the 40,000-ton luxury liner, the Hedonist,
it was going due west at a speed of 20 knots in calm seas through a rare
fog just before it was struck broadside by the 60,000-ton freighter, the
Ironhorse, which was traveling north at 10 knots. The transmission also
noted that when the freighter's bow pierced the hull of the liner, the
two ships stuck together and sank together.
- You have been hired to check the technical correctness of an
upcoming made-for-TV murder mystery that takes place in the space
shuttle. In one scene, an astronaut's safety line is cut while on a
space walk. The astronaut, who is 200 meters from the shuttle and not
moving with respect to it, finds that the suit's thruster pack has also
been damaged and no longer works and that only 4 minutes of air remains.
To get back to the shuttle, the astronaut unstraps a 10-kg tool kit and
throws it away with a speed of 8 m/s. In the script, the astronaut, who
has a mass of 80 kg without the toolkit, survives, but is this correct?
- You have been hired as a technical consultant for an
early-morning cartoon series for children to make sure
that the science is correct. In the script, a wagon
containing two boxes of gold (total mass of 150 kg) has
been cut loose from the horses by an outlaw. The wagon
starts from rest 50 meters up a hill with a 6o slope. The
outlaw plans to have the wagon roll down the hill and
across the level ground and then crash into a canyon
where his confederates wait. But in a tree 40 meters from
the edge of the canyon wait the Lone Ranger (mass 80 kg)
and Tonto (mass 70 kg). They drop vertically into the
wagon as it passes beneath them. The script states that
it takes the Lone Ranger and Tonto 5 seconds to grab the
gold and jump out of the wagon, but is this correct?. You
assume that the wagon rolls with negligible friction.
- You are helping your friend prepare for the next skateboard
exhibition by determining if the planned program will work. Your friend
will take a running start and then jump onto a heavy-duty 15-lb
stationary skateboard. The skateboard will glide in a straight line
along a short, level section of track, then up a sloped concrete wall.
The goal is to reach a height of at least 10 feet above the starting
point before coming back down the slope. Your friend's maximum running
speed to safely jump on the skateboard is 23 feet/second. Your friend
weighs 150 lbs.
- Because of your physics background, you have been hired
as a technical advisor for a new James Bond adventure
movie. In the script, Bond and his latest love interest,
who is 2/3 his weight (including skis, boots, clothes,
and various hidden weapons), are skiing in the Swiss
Alps. She skis down a slope while he stays at the top to
adjust his boot. When she has skied down a vertical
distance of 100 ft, she stops to wait for him and is
captured by the bad guys. Bond looks up and sees what is
happening. He notices that she is standing with her skis
pointed downhill while she rests on her poles. To make as
little noise as possible, Bond starts from rest and
glides down the slope heading right at her. Just before
they collide, she sees him coming and lets go of her
poles. He grabs her and they both continue downhill
together. At the bottom of the hill, another slope goes
uphill and they continue to glide up that slope until
they reach the top of the hill and are safe. The writers
want you to calculate the maximum possible height that
the second hill can be relative to the position where the
collision took place. Both Bond and his girl friend are
using new, top-secret frictionless stealth skis developed
for the British Secret Service.
- Because of your concern that incorrect science is being
taught to children when they watch cartoons on TV, you
have joined a committee which is reviewing a new cartoon
version of Tarzan. In this episode, Tarzan is on the
ground in front of a herd of stampeding elephants. Just
in time Jane, who is up in a tall tree, sees him. She
grabs a convenient vine and swings towards Tarzan, who
has twice her mass, to save him. Luckily, the lowest
point of her swing is just where Tarzan is standing. When
she reaches him, he grabs her and the vine. They both
continue to swing to safety over the elephants up to a
height which looks to be about 1/2 that of Jane's
original position. To decide if you going to approve this
cartoon, calculate the maximum height Tarzan and Jane can
swing as a fraction of her initial height.
- You are watching a Saturday morning cartoon concerning a
jungle hero called George of the Jungle. George attempts
to save his friend, an ape named Ape, from a stampeding
herd of wildebeests. Ape is at the base of a tall tree
which has a vine attached to its top. George is in
another tree holding the other end of the vine. George
plans to swing down from the tree, grab Ape at the bottom
of the swing, and continue up to safety on a ledge which
is half of George's initial height in the tree. Assuming
that Ape weighs the same as George, will they
successfully make it to the top of the ledge?
- Your friend has just been in a traffic accident and hopes that
you can show the accident was the other drivers fault. Your friends
car was traveling North when it entered the intersection. When it
reached the center of the intersection, the car was struck by the other
drivers car which was traveling East. The two cars remained joined
together after the collision and skidded to a stop. The speed limit on
both roads is 50 mph. From the skid marks still visible on the street,
you determine that after the collision the cars skidded 56 feet at an
angle of 30 degrees north of east before stopping. The police report gives the
make and year of each car. The weight of your friends car is 2600 lbs
and that of the other car is 2200 lbs, including the drivers weight in
each case. The coefficient of kinetic friction for a rubber tire
skidding on dry pavement is 0.80. You decide to see if the other driver
was speeding and if your friend was under the speed limit.
- Because movie producers have come under pressure for
teaching children incorrect science, you have been
appointed to help a committee of concerned parents review
a script for a new Superman movie. In the scene under
consideration, Superman rushes to save Lois Lane who has
been pushed from a window 300 feet above a crowded
street. Superman is 0.5 miles away when he hears Lois
scream and rushes to save her. He swoops down in the nick
of time, arriving when Lois is just 3.0 feet above the
street, and stopping her just at ground level. Lois
changes her expression from one of horror at her
impending doom to a smile of gratitude as she gently
floats to the ground in Superman's arms. The committee
wants to know if there is really enough time to express
this range of emotions, even if there is a possible
academy award on the line. The chairman asks you to
calculate the time it takes for Superman to stop Lois's
fall. To do the calculation, you assume that Superman
applies a constant force to Lois in breaking her fall and
that she weighs 120 lbs. While thinking about this scene
you also wonder if Lois could survive the force that
Superman applies to her.
- This year you have a summer job working for the National
Park Service. Since they know that you have taken
physics, they start you off in the laboratory which tests
possible new equipment. Your first job is to test a small
cannon. During the winter, small cannons are used to
prevent avalanches in populated areas by shooting down
heavy snow concentrations overhanging the sides of
mountains. In order to determine the range of the cannon,
it is necessary to know the velocity with which the
projectile leaves the cannon (muzzle velocity). The
cannon you are testing has a weight of 700 lbs and shoots
a 40-lb projectile. During the lab tests the cannon is
held horizontally in a rigid support so that it cannot
move. Under those conditions, you measure the magnitude
of the muzzle velocity to be 400 m/s. When the cannon is
actually used in the field, however, it is mounted so
that it is free to move (recoil) when it is fired. Your
boss asks you to calculate the projectile's speed leaving
the cannon under field conditions, when it is allowed to
recoil. She tells you to take the case where the cannon
is fired horizontally using cannon shells which are
identical to those used in the laboratory test.
- For a part time job with a medical physics group, you are
studying a cancer therapy that uses neutrons to knock a particle out of
the nucleus of the atoms of cancer cells. This is an inelastic collision
in which the heavy nucleus essentially does not move. After the
collision, the nucleus decays and kills the cancer cell. You decide to
measure the change in internal energy of a nitrogen nucleus after a
neutron collides with it. In the experiment, a neutron hits the nucleus
with a speed of 2.0 x 10^7 m/s and you detect two neutrons both coming
out at angles of 30 degrees with respect to the direction that the neutron
coming in.
Note: Each problem begins with a list of the specific principles necessary to solve the context-rich problem. These are for the benefit of the instructor. Delete the list before using the problems in your class.
- Center of Mass: You have been hired as part of a
research team consisting of biologists, computer
scientists, engineers, mathematicians, and physicists
investigating the virus which causes AIDS. This effort
depends on the design of a new centrifuge which separates
infected cells from healthy cells by spinning a container
of these cells at very high speeds. Your design team has
been assigned the task of specifying the mechanical
structure of the centrifuge arm which holds the sample
container. For aerodynamic stability, the arm must have
uniform dimensions. Your team decided the shape will be a
long, thin strip of length L, width w, and thickness t.
The mass of the strip is M. The actual values of these
quantities will be optimized by a computer program. For
mechanical reasons, the arm must be stronger at one end
than at the other. Your team decided to use new composite
materials to accomplish this. Using these materials
changes the strength by changing the density of the arm
along its length while keeping its dimensions constant.
To calculate the strength of the brackets necessary to
support the arm, you must determine the position of the
center of mass of the arm. You decide to do this in two
different ways.
(a) First you make a crude approximation of your design by assuming that the arm is a rigid, massless rod of length L. On this rod are mounted four small objects of equal mass. One of these objects is positioned at each end of the rod, one in the center of the rod, and one midway between the center and the end.
(b) Next you do a more exact calculation by assuming that arm is a continuous material with a density which varies linearly along its length as (A + Bx).
- Center of Mass, Moment of Inertia: You are on a
development team investigating a new design for computer
magnetic disk drives. You have been asked to determine if
the standard disk drive motor will be sufficient for the
test version of the new disk. To do this you decide to
calculate how much energy is needed to get the 6.4 cm
diameter, 15 gram disk to its operating speed of 350
revolutions per second. The test disk also has 4
different sensors attached to its surface. These small
sensors are arranged at the corners of a square with
sides of 1.2 cm. To assure stability, the center of mass
of the sensor array is in the same position as the center
of mass of the disk. The disk's axis of rotation also
goes through the center of mass. You know that the
sensors have masses of 1.0 grams, 1.5 grams, 2.0 grams,
and 3.0 grams. The moment of inertia of your disk is
one-half that of a ring.
- Center of Mass, Momentum, Kinematics: Two
government agents (FBI agents Mulder and Scully) need
your physics expertise to determine why an alien
spaceship exploded. The wreckage of the spaceship is in
three large pieces around a northern Minnesota town. The
center of mass of one piece (mass = 300 kg) of the
spaceship landed 6.0 km due north of the center of town.
Another piece (mass = 1000 kg) landed 1.6 km to the
southeast (36 degrees south of east) of the center of
town. The last piece (mass = 400 kg) landed 4.0 km to the
southwest (65 degrees south of west) of the center of
town. There are no more pieces of the spaceship. The
Army, which was watching the spaceship on its radar,
claims it was hovering motionless over the center of town
when the spaceship spontaneously exploded and the pieces
fell to the ground. Agents Mulder and Scully do not
believe that the spaceship exploded on its own accord.
They think a missile hit it. They ask you to determine
whether the fragments found are consistent with the
spaceship exploding spontaneously. If not, determine from
what direction the missile came. (For simplicity, assume
that the pieces of the spaceship after the explosion are
moving horizontally.)
- Kinematics, Moment of Inertia: You are working in
a research group investigating more energy efficient city
busses. One option is to store energy in the rotation of
a flywheel when the bus stops and then use it to
accelerate the bus. The flywheel under consideration is
disk of uniform construction except that it has a
massive, thin rim on its edge. Half the mass of the
flywheel is in the rim. When the bus stops, the flywheel
needs to rotate at 20 revolutions per second. When the
bus is going at its normal speed of 30 miles per hour,
the flywheel rotates at 2 revolutions per second. The
material holding the rim to the rest of the flywheel has
been tested to withstand an acceleration of up to 100g
but you are worried that it might not be strong enough.
To check, you calculate the maximum radius of the rim for
the case when the flywheel reaches 20 revolutions per
second just as the bus going 30 miles per hour makes an
emergency stop in 0.50 seconds. You assume that during
this time the flywheel has a constant angular
acceleration. Your trusty physics text tells you that the
moment of inertia of a disk rotating about its center is
half that of a ring of the same mass and radius.
- Kinematics, Force: You did so well in your physics
course that you decided to try to get a summer job
working in a physics laboratory at the University. You
got the job as a student lab assistant in a research
group investigating the ozone depletion at the Earth's
poles. This group is planning to put an atmospheric
measuring device in a satellite which will pass over both
poles. To collect samples of the upper atmosphere, the
satellite will be in a circular orbit 200 miles above the
surface of the Earth which has a radius of about 4000
miles. To adjust the instruments for the proper data
taking rate, you need to calculate how many times per day
the device will sample the atmosphere over the South
pole.
- Kinematics, Force: While listening to your
professor drone on, you dream about becoming an engineer
helping to design a new space station to be built in deep
space far from any planetary systems. This
state-of-the-(future) art station is powered by a small
amount of neutron star matter which has a density of 2 x
1014 g/cm3. The station will be a large light-weight
wheel rotating about its center which contains the power
generator. A control room is a tube which goes all the
way around the wheel and is 10 meters from its center.
The living space and laboratories are located at the
outside rim of the wheel and are another tube which goes
all the way around it at a distance of 200 meters from
the center. To keep the environment as normal as
possible, people in both the outer rim and the control
room should experience the same “weight” as
they had on Earth. That is if they were standing on a
bathroom scale, it would read the same as if they were on
Earth. This is accomplished by a combination of the
rotation of the station and the gravitational attraction
of the neutron star matter in the power generator. You
suddenly wake up when you drop your pen but decide that
the idea is interesting enough to calculate the necessary
rate of rotation and generator mass. While drawing the
free-body diagrams, you realize that the people are
standing with their heads inward on the rim of the
station and with their heads outward in the control room.
- Kinematics, Force: You have a summer job at NASA
where your team is responsible for specifying a rocket to
lift a communications satellite into a circular orbit
around the Earth. To effectively relay signals, the
satellite will have to always remain over the same point
on the Earth's equator just above the communications
station which is located 50 miles outside or Nairobi,
Kenya. The satellite will have a mass of 3500 kg. You
have been assigned the task of calculating the radius of
the satellite's orbit and its speed while in orbit and
presenting that calculation to your team. For your own
curiosity you also decide to calculate the force that the
satellite exerts on the Earth while it is in orbit. From
your trusty physics textbook you find the radius of the
Earth is 6370 km, its mass is 5.96 x 1024 kg, and the
universal gravitational constant is 6.67 x 10-11 N
m2/kg2.
- Energy: While working in an environmental
engineering team to determine the quality of the air in
downtown Minneapolis, you have been given the task of
calibrating the spectrum analyzer. This device gives you
the composition of the gasses in a sample by determining
the frequency of light absorbed by the sample. Each type
of molecule absorbs a certain set of frequencies (its
spectrum). The frequencies actually measured are changed
if the molecules have an angular velocity about their
center of mass. To calibrate the analyzer, you must
calculate the expected angular velocity for the Oxygen
molecules (O2) in the sample of Minneapolis air. At the
temperatures of your gas sample, you calculate that the
center of mass speed of a typical molecule is 500 m/s.
Based on you knowledge of atomic sizes, you estimate that
the typical distance between the nuclei of oxygen atoms
in the molecule is 10-8 cm. You also know that the 27 x
10-27 kg mass of an Oxygen atom is essentially
concentrated in its very small nucleus. Your boss tells
you to assume that the rotational kinetic energy of the
molecule rotating about an axis through the center of the
line joining the nuclei of the atoms and perpendicular to
that line is 2/3 its translational kinetic energy.
- Energy: While working on your latest novel about
settlers crossing the Great Plains in a wagon train, you
get into an argument with your co-author regarding the
moment of inertia of an actual wooden wagon wheel. The
70-kg wheel is 120-cm in diameter and has heavy spokes
connecting the rim to the axle. Your co-author claims
that you can approximate using I = MR2 (like for a
hoop) but you anticipate I will be
significantly less than that because of the mass located
in the spokes. To find I experimentally, you mount
the wheel on a low-friction bearing then wrap a light
cord around the outside of the rim to which you attach a
20-kg bag of sand. When the bag is released from rest, it
drops 3.77-m in 1.6-s during which time the wheel rotates
through an angle of 2¹-radians. Hint: Use energy
considerations.
- Energy: You have a summer job helping to design
the opening ceremony for the next winter Olympics. One of
the choreographer's ideas is to have skaters race out
onto the ice and grab a very large ring (the symbol of
the Olympics). Each ring is held horizontal at shoulder
height by a vertical pole stuck into the ice. The pole is
attached to the ring on its circumference so that the
ring can rotate horizontally around the pole. The plan is
to have the skater grab the ring at a point on the
opposite side from where the pole is attached and,
holding on, glide around the pole in a circle. You have
been assigned the job of determining the minimum speed
that the skater must have before grabbing the ring in
terms of the radius of the ring, the mass of the ring,
the mass of the skater, and the constant frictional force
between the skates and the ice. The choreographer wants
the skater and ring to go around the pole at least five
times. The skater is to be moving tangent to the ring
just before grabbing it.
- Energy, Center of Mass: As a project your team is
given the task of designing a space station consisting of
four different habitats. Each habitat is an enclosed
sphere containing all necessary life support and
laboratory facilities. The masses of these habitats are
10 x 105 kg, 20 x 105 kg, 30 x 105 kg, and 40 x 105 kg.
The entire station must spin so that the inhabitants will
experience an artificial gravity. Your team has decided
to arrange the habitats at corners of a square with 1.0
km sides. The axis of rotation will be perpendicular to
the plane of the square and through the center of mass.
To help decide if this plan is practical, you calculate
how much energy would be necessary to set the space
station spinning at 5.0 revolutions per minute. In your
team's design, the size of each habitat is small compared
to the size of the space between the habitats and the
structure that holds the habitats together is much less
massive than any single habitat.
- Energy, Center of Mass: You have a great summer
job working for a movie studio. Your assignment is to
check the script of an upcoming Star Wars movie for
scientific accuracy. In one scene, the hero escapes by
putting her spaceship through a wormhole in space. The
engines have failed so the ship is coasting when it
emerges in another part of the galaxy at the center of a
binary star system. Both stars in the system orbit their
center of mass and have equal mass. You need to determine
the minimum speed of the spaceship when it emerges from
the wormhole perpendicular to the plane of the orbiting
stars so that it is not captured by the star system. When
the movie is better defined, you will know the mass of
each star, the radius of their orbit, and the mass of the
spaceship. You assume that even a long time ago in a
galaxy far, far away the gravitational constant is the
same.
- Energy, Forces: You have applied for a great
summer job working with a special effects team at a movie
studio. As part of your interview you have been asked to
evaluate the design for a stunt in a new Indiana Jones
production. A large spherical boulder starts from rest
and rolls down an inclined track. At the bottom, the
track curves up into a vertical circle so that the
boulder can roll around on the inside of the circle and
come back to ground level. It is important that the
boulder not fall off the track at the top of the circle
and crush the star standing below. You have been asked to
determine the relationship between the height of the
boulder's starting point on the ramp (measured from the
center of the boulder) and the maximum radius the
circular part of the track. You can determine the mass
and the radius of the boulder should you need to know
them. You have also been told that the moment of inertia
of a sphere is 2/5 that of a ring of the same mass and
radius. After some thought you decide that the boulder
will stay moving in a vertical circle if its radial
acceleration at the top is just that provided by gravity.
- Torque: In a budget cutting move, the University
decided to replace their human mascot, Goldie Gopher, by
a real gopher. Unfortunately the new 10 lb Goldie has
other ideas and has escaped the clutches of the athletic
department by jumping out a window onto a flagpole
attached to the building. The fire department has been
called in to recover the recalcitrant gopher. The plan is
for a fireman to climb out on the flagpole and get
Goldie. Goldie is 3 meters out on the 4 meter long
flagpole. Because of your technical background, you have
a part time job as a University safety officer and are
asked to approve this plan. The pole is attached to the
building at an angle of 37º above the horizontal and
weighs 22 lbs. A horizontal cable with a rated strength
of 300 lbs connects the far end of the pole to the
building seems strong enough. The other end of the pole
is connected to the building by a steel pin supported by
a strong steel brace. You are worried about whether this
pin is strong enough so you calculate the forces on the
pin. The lightest fireman available for the job of
getting Goldie weighs 150 lbs in all of her gear.
You find that the pin is strong enough so you might approve this daring rescue. You want it to be as safe as possible. You will require that the fireman wear a safety harness which is held by someone inside the building. After all, the cable holding up the flagpole has been out in the Minnesota winter for years. If the cable does break, the flagpole will rotate about the pin supporting its base.
Doing a quick integral, you find that the moment of inertia of a pole about an axis at one end is 1/3 as much as if all its mass were concentrated at the other end of the pole. To save the fireman you must get her off before the pole goes below a horizontal orientation. The gopher will be on its own. To see if rescue is possible, you calculate the acceleration of the flagpole with the fireman and gopher clinging to it for the two extreme cases, just after the cable breaks and just as it reaches a horizontal orientation.
- Torque: The automatic flag raising system on a
horizontal flagpole attached to the vertical outside wall
of a tall building has become stuck. The management of
the building wants to send a person crawling out along
the flagpole to fix the problem. Because of your physics
knowledge, you have been asked to consult with a group to
decide whether or not this is possible. You are all too
aware that no one could survive the 250 foot fall from
the flagpole to the ground. The flagpole is a 120 lb
steel I-beam which is very strong and rigid. One side of
the flagpole is attached to the wall of the building by a
hinge so that it can rotate vertically. Nine feet away,
the other end of the flagpole is attached to a strong,
lightweight cable. The cable goes up from the flagpole at
an angle of 30º until it reaches the building where it
is bolted to the wall. The mechanic who will climb out on
the flagpole weighs 150 lbs including equipment. From the
specifications of the building construction, both the
bolt attaching the cable to the building and the hinge
have been tested to hold a force of 500 lbs. Your boss
has decided that the worse case is when the mechanic is
at the far end of the flagpole, nine feet from the
building.
- Torque: After watching a news story about a fire
in a high rise apartment building, you and your friend
decide to design an emergency escape device from the top
of a building. To avoid engine failure, your friend
suggests a gravitational powered elevator. The design has
a large, heavy turntable (a horizontal disk that is free
to rotate about its center) on the roof with a cable
wound around its edge. The free end of the cable goes
horizontally to the edge of the building roof, passes
over a heavy vertical pulley, and then hangs straight
down. A strong wire cage which can hold 5 people is then
attached to the hanging end of the cable. When people
enter the cage and release it, the cable unrolls from the
turntable lowering the people safely to the ground. To
see if this design is feasible you decide to calculate
the acceleration of the fully loaded elevator to make
sure it is much less than g. Your friend's design has the
radius of the turntable disk as 1.5 m and its mass is
twice that of the fully loaded elevator. The disk which
serves as the vertical pulley has 1/4 the radius of the
turntable and 1/16 its mass. In your trusty Physics book
you find that the moment of inertia of a disk is 1/2 that
of a ring.
- Torques, Kinematics: Because of your physics
background, you have been asked to be a stunt consultant
for a motion picture about a genetically synthesized
prehistoric creature that escapes from captivity and
terrorizes the city. The scene you are asked to review
has the three main characters of the movie being chased
by the creature through an old warehouse. At the exit of
the warehouse is a thick steel fire door 10 feet high and
6.0 feet wide weighing about 2,000 pounds. In the scene,
the three actors are to flee from the building and close
the fire door (initially at rest), thus sealing the
creature inside the building. With the creature running
at 30 mph, they have 5.0 seconds to shut the door. You
are asked to determine if they can do it. You estimate
that each actor can each push on the door with a force of
50 pounds. When they push together, each actor needs a
space of about 1.5 feet between them and the next actor.
The door, which has a moment of inertia of 1/3 M r2
around its hinges, needs to rotate 120 degrees for it to
close completely.
- Torque, Kinematics: While watching the local TV
news show, you see a report about ground water
contamination and how it effects farms which get their
water from wells. For dramatic effect, the reporter
stands next to an old style well which still works by
lowering a bucket at the end of a rope into a deep hole
in the ground to get water. At the top of the well a
single vertical pulley is mounted to help raise and lower
the bucket. The thin rope passes over the large pulley
which is essentially a heavy steel ring supported by
light spokes. To demonstrate the depth of the well, the
reporter completely wraps the rope around the pulley and
suspends the bucket from one end. She then releases the
bucket, at rest near the pulley, and it descends to the
bottom of the well unwinding the rope from the pulley as
it falls. It takes 2.5 seconds. She doesn't tell you the
depth of the well so you decide to calculate it. You
estimate that the pulley has the same mass of the bucket
and assume that the mass of the rope and any friction can
be neglected.
- Energy or Torques, Kinematics: While you watching
a TV show about life in the ancient world, you see that
the people in one village used a solid sphere made out of
clay as a kind of pulley to help haul up water from a
well. A well-greased wooden axle was placed through the
center of the sphere and fixed in a horizontal
orientation above the well, allowing the sphere to rotate
freely. To demonstrate the depth of the well, the host of
the program completely wrapped the rope around the sphere
and suspended the bucket from one end. She then released
the bucket, at rest near the sphere, and allowed it to
descend to the bottom of the well unwinding the string
from the sphere as it went. It took 2.5 seconds. You
wonder what the depth of the well was so you decide to
calculate it. You estimate that the sphere has twice the
mass of the bucket and assume that the mass of the rope
can be neglected. You look up the moment of inertia of a
sphere about an axis through its center of mass and find
it is 2/5 that of a ring of the same mass and radius.
- Energy or Torque, Kinematics: You have been asked
to help design a safety mechanism which will
automatically drops a rope from the window of an
apartment in the case of fire. One end of the rope is
fastened to a ledge on the outside wall of the building
while the other is rolled tightly around a hollow
cylinder. When a fire is detected, the mechanism drops
the hollow cylinder so that it is parallel to the ground.
The cylinder falls straight down without touching the
side of the building and the rope unwinds from around a
point midway along its length. To optimize your design,
you need to calculate how long it takes to fall to the
ground as a function of the height of the fall, the
radius of the cylinder, the mass of the cylinder, and the
length of the cylinder.
- Torques, Forces: A friend of yours who likes to
fix his own car has improvised a car-lifting device in
his garage. He explains that he plans to park the car on
a rectangular platform which is lifted into the air by
four ropes each attached to a corner of the platform. The
platform is constructed of steel I-beams and has a weight
of 250 lbs. It is 12 feet long and 5.0 feet wide with its
center of mass 5.0 feet from the front and 2.5 feet from
either side. His car has a weight of 1400 lbs and 75% of
that weight is carried by the front tires. The distance
between the centers of the tires is 7.2 feet. His plan is
to park the car in the middle of the platform with the
front tire 2.4 feet from the front of the platform over
the midpoint of the platform. In that way, the two front
ropes have the equal tensions and the two back ropes will
also have equal tensions. The ropes are certified to hold
a load of 5000 N each. Before he uses his device, he has
asked your advice on its safety.
- Torques, Forces: You have been asked to design a
machine to move a large cable spool up a factory ramp in
30 seconds. The spool is made of two 6.0 ft diameter
disks of wood with iron rims connected together at their
centers by a solid cylinder 1.0 ft wide and 3.0 ft long.
Sometime later in the manufacturing process, cable will
be wound around the cylinder. For now the cylinder is
bare but the spool still weighs 200 lbs. Your plan is to
attach a thin ring around the cylinder and pull the spool
up the ramp with a rope attached to the top of this ring.
The spool will then roll without slipping up the ramp on
its two outside disks at a constant speed. To finish the
design you need to calculate how strong the rope must be
to pull the spool when it is moving up the ramp at a
constant speed. The ramp has an angle of 27o from the
horizontal and the rope will be parallel to the ramp. A
set of light weight bearings minimizes the friction
between the ring and the cylinder and fixes the
orientation of the ring so that the rope always pulls
from its top. The diameter of the ring is essentially the
same as that of the cylinder.
- Torques, Forces: You have been chosen to be part
of a team investigating an explosion in a virology
laboratory. When you enter the lab, you see that a large
utility conduit, which was originally suspended
horizontally overhead, has fallen on top of a chemical
workbench. You decide to determine if a mechanical
failure made the conduit break, crashing into the
chemicals and causing the explosion or if the chemical
explosion caused the conduit to fall. The heavy conduit,
essentially a bar with a non-uniform mass distribution,
was held up in the air by two lightweight cables attached
to the ceiling at different angles. One cable was
attached at each end of the conduit. To check out the
possibility of a mechanical failure, you first decide to
calculate the position of the center of mass from one end
of the conduit based on the known weight of the conduit,
the length of the conduit, and the angles of the cables
with the ceiling.
- Torques, Forces: You have a summer job working
downtown washing windows on skyscrapers (the pay is great
and so are the medical benefits). The platform you and
your partner are using to get to the windows is a meter
wide and four meters long. You know from hauling the
platform out of your truck countless times that it has a
mass of 70 kg. It is supported by two cables, one at each
end, mounted on-center to prevent the platform from
tipping over as it is pulled up the side of the building
at a constant speed. If you (mass of 55 kg) are standing
on the platform 1 meter from one cable while your partner
(mass of 87 kg) is 1.3 meters from the other cable and
both of you are half a meter from the side, what is the
tension in each cable? Assume the platform has a uniform
mass distribution and is of negligible thickness.
- Angular Momentum: You are part of a team in an
engineering contest trying to design a mechanical
"cat" which, when dropped motionless, upside
down from 2.5 m, can right itself before it hits the
ground by rotating its "tail." The body of the
"cat," aptly named Katt, is a solid cylinder 1
foot in length and 6 inches in diameter, with a mass of
5.44 kg. Attached to the center of one end of the body is
Katt's "tail," a 1 foot long rod which extends
out perpendicular to Katt's body and has only 1% the mass
of the body. Your task is to determine the energy demand
put on the small electric motor in the body which rotates
the "tail." Based on your work, have you any
design improvements to suggest to the rest of the team?
Remember: a solid cylinder rotated about it's central
axis has a moment of inertia 1/2 that of a cylinder with
all it's mass on it's circumference; a rod rotated about
one end has a moment of inertia 1/3 of that if mass were
concentrated at the opposite end.
- Angular Momentum: You have been asked to help
evaluate a proposal to build a device to determine the
speed of hockey pucks shot along the ice. The device
consists of a rod which rests on the ice and is fastened
to the ice at one end so that it is free to rotate
horizontally. The free end of the rod has a small, light
basket which will catch the hockey puck. The puck slides
across the ice perpendicular to the rod and is caught in
the basket which is initially at rest. The rod then
rotates. The designers claim that knowing the length of
the rod, the mass of the rod, the mass of the puck, and
the frequency of the rotation of the rod and puck, you
can determine the speed of the puck as it moved across
the ice.
- Angular Momentum, Energy: You are a member of a
group designing an air filtration system for allergy
suffers. To optimize its operation you need to measure
the mass of the common pollen in the air where the filter
will be used. To measure the pollen's mass, you have
designed a small rectangular box with a hole in one side
to allow the pollen to enter. Once inside the pollen is
given a positive electric charge and accelerated by an
electrostatic force to a speed of 1.4 m/s. The pollen
then hits the end of a very small, uniform bar which is
hanging straight down from a pivot at its top. Since the
bar has a negative charge at its tip, the pollen sticks
to it as the bar swings up. Measuring the angle that the
bar swings up would give the particle's mass. After the
angle is measured, the charge of the bar is reversed,
releasing that particle. It's a cool design but your
friend insists it will never work. To prove it she asks
you to calculate the length of the bar which would give
you a reasonable angle of about 10º for a typical pollen
particle of 4 x 10-9 grams. Your plan calls for a bar of
7 x 10-4 grams with a moment of inertial 1/12 as much as
if all of its mass were concentrated at its end. Is she
right?
- Angular Momentum, Energy: You have been asked to
design a new stunt for the opening of an ice show. A
small 50 kg skater glides down a ramp and along a short
level stretch of ice. While gliding along the level
stretch she makes herself as small as possible. Keeping
herself as small as possible she then grabs the bottom
end of a large 180 kg vertical rod which is free to turn
vertically about a axis through its center. The plan is
for her to hold onto the 20 foot long rod while it swings
her to the top. The rod has a uniform mass distribution.
You have been asked to give the minimum height of the
ramp. Doing a quick integral tells you that the moment of
inertia of this rod about its center is 1/3 of what its
moment of inertia would be if all of its mass were
concentrated at one of its ends.
- Angular Momentum, Energy: Your group has decided
to revisit the lab experiment in which a metal ring was
dropped onto a rotating plate. In hopes of getting better
results, you now have a motor which initially spins the
disk and shaft at 3.0 rev. per second. You are also using
a mechanical device to drop the ring, so that it lands
perfectly in the groove on every trial. Unfortunately the
bearing in your apparatus is giving out (after weeks of
heavy use) so you must redo your analysis, taking into
account the frictional force which the bearing applies to
the outside of the shaft. You assume that this force is
approximately constant, except perhaps during the
collision event itself. To avoid the large uncertainties
associated with using a stopwatch, you decide to count
revolutions -- you let the disk rotate twice after
disengaging the motor, then drop the ring, then note that
the entire apparatus goes around 17 more times before
coming to rest. How large is the frictional force? The
radii of the disk, shaft, and ring are 11 cm, 0.63 cm,
and 6.5 cm (5.5 cm) outside (inside) respectively. The
moments of inertia (about the appropriate axis) for the
disk, shaft, and ring are 5.1 x 10-3 kg m2, 3.7 x 10-6 kg
m2, and 8.9 x 10-3 kg m2 respectively.
- Angular Momentum, Energy, Kinematics: You have been hired by a company which is designing a new water slide for an amusement park . The conceptual design has a customer going down a curved slide ending up moving horizontally at the bottom. At the end of the of the slide, the customer grabs the end of a 16.0 m long vertical bar that is free to pivot about its center. After grabbing onto the bar, the customer swings out over a pool of water. When the bar swings out to its maximum distance, the customer can drop off and fall straight down into the water. Your task is to determine the height of the slide so that the maximum horizontal distance that the bar swings out is 5.0 m for a 60 kg person. The bar has five times the mass of a 60 kg person. From an engineering handbook, you find that the moment of inertia of the bar is 1/12 of what it would be if all of its mass were concentrated at the bottom.
- To take a break from studying physics, you rent the video
of the movie version of the book Fahrenheit 451,
which stared Oscar Werner. The setting (in England) is an
Orwellian society where books are banned and all
information is disseminated by a large TV screen in each
home. Fire departments respond not to put out fires, but
to burn books, which combust at a temperature of 451 °F
(hence the name of the film). In the middle of the film,
your mind wanders. You imagine the fire department using
the burning books to heat 600 cm3 of water for their
afternoon tea. You imagine that the burner transfers 80%
of the heat from the burning books to the water, which
you remember has a heat capacity of 1.0 calorie/g oC. How
much will the water temperature rise from burning one
copy of the 500-page book Fahrenheit 451 if the
heat of combustion is 1.0 calorie per page?
- You are helping a friend who is a veterinarian to do some
minor surgery on a cow. She has asked you to sterilize a
scalpel and a hemostat by boiling them for 30 minutes.
You boil them as ordered and then quickly transfer the
instruments to a well insulated tray containing 200 grams
of sterilized water at room temperature (23 °C) which is
just enough to cover the instruments. After a few minutes
the instruments and water will come to the same
temperature, but will they be safe to hand to your friend
without being burned? You are both wearing surgical
rubber gloves, but they are very thin. You know that both
the 50 gram scalpel and the 70 gram hemostat are made
from steel which has a specific heat of 450 J / (kg °C).
They were boiled in 2.0 kg of water with a specific heat
of 4200 J / (kg °C).
- You have a summer job with a company that designs
cookware. Your group is assigned the task of designing a
better pasta pot. You are very excited by a new strong,
light alloy the group has just produced, but will it make
a good pasta pot? If it takes more than 10 minutes to
boil water in a pasta pot, it probably won't sell. So
your boss asks you to calculate how long it would take
water at room temperature (23 °C) to reach boiling
temperature (100 °C) in a pot made of the new alloy. Your
colleagues tell you that a typical pasta pot holds about
2 liters (2.0 kg) of water. They estimate that a pot made
of the alloy would have a mass of 550 grams, and a
specific heat capacity of 860 J / (kg °C). You look in
your physics book and find that water has a specific heat
capacity of 4200 J / (kg °C) and its heat of vaporization
is 2.3 x 106 J/kg. The owner's manual states that the
burners on your stove deliver 1000 Joules of heat per
second. You estimate that only about 20% of this heat is
radiated away.
- You are planning a birthday party for your niece and need
to make at least 4 gallons of Kool-Aid, which you would
like to cool down to 32 oF (0 °C) before the party
begins. Unfortunately, your refrigerator is already so
full of treats that you know there will be no room for
the Kool-Aid. So, with a sudden flash of insight, you
decide to start with 4 gallons of the coldest tap water
you can get, which you determine is 50 °F (10 °C), and
then cool it down with a 1-quart chunk of ice you already
have in your freezer. The owner's manual for your
refrigerator states that when the freezer setting is on
high, the temperature is -20 °C. Will your plan work? You
assume that the density of the Kool-Aid is about the same
as the density of water. You look in your physics book
and find that the density of water is 1.0 g/cm3, the
density of ice is 0.9 g/cm3, the heat capacity of water
is 4200 J / (kg °C), the heat capacity of ice is 2100 J /
(kg °C), the heat of fusion of water is 3.4 x 105 J/kg,
and its heat of vaporization is 2.3 x 106 J/kg.
- You are thinking ahead to spring when one of your friends
is having an outdoor wedding. Your plan is to design the
perfect lemonade for the event. The problem with lemonade
is that you make it at room temperature and then add ice
to cool it to a pleasant 10 °C. Usually, the ice melts
diluting the lemonade too much. To help you solve this
problem, you look up the specific heat capacity of water
(1.0 cal/(gm °C)), the specific heat capacity of ice
(0.50 cal/(gm °C)), and the latent heat of fusion of
water (80 cal/gm). You assume that the specific heat
capacity of the lemonade is the same as water. Since you
will cool your lemonade in a Thermos jug, assume no heat
is added to the lemonade from the environment. Using that
information, you calculate how much water you get from
all the ice melting if you make 6 quarts (5.6 kg) of
lemonade at room temperature (23 °C) and add ice which
comes straight from the freezer at -5.0 °C.
- While working for a grain loading company over the
summer, your boss asks you to determine the efficiency of
a new type of pneumatic elevator. The elevator is
supported in a cylindrical shaft by a column of air,
which you assume to be an ideal gas with a specific heat
of 12.5 J/mol-°C. The air pressure in the column is 1.2
x 105 Pa when the elevator carries no load. The bottom of
the cylindrical shaft opens out so that there is a
reservoir of air at room temperature (25° C) below the
elevator when it begins loading. Seals around the
elevator assure that no air escapes as the elevator moves
up and down. The elevator has a cross-sectional area of
10 m2. A cycle of elevator use begins with the unloaded
elevator. The elevator is then loaded with 20,000 kg of
grain while the air temperature stays at 25° C causing
the elevator to sink. The air in the system is then
heated to 75° C and the elevator rises. The elevator is
then unloaded, while the air remains at 75° C. Finally,
the air in the system is cooled to room temperature
again, returning the elevator to its starting level.
While the elevator is moving up and down, you assume that
it moves at a constant velocity so that the pressure in
the gas is constant.
- Note: This problem requires both mechanical energy and
heat energy for a solution. In the class demonstration, a
2.0-gram lead bullet was shot into a 2.0-kg block of
wood. The block of wood with the bullet stuck in it was
hung from a string and rose to a height 0.50 cm above its
initial position. From that information we calculated
that the initial speed of the bullet was about 300 m/s
(close to the speed of sound). What was the bullet like
when it stopped? Using conservation of energy and
conservation of momentum, we decided that the internal
energy of the bullet, block system had increased
substantially. If the change of internal energy of the
bullet was half that of the system, would this change be
enough to melt the bullet? Assume that the bullet had a
temperature of 50 °C when it left the gun. The melting
temperature of lead is 330 °C. It has a specific heat
capacity of 130 J/(kg °C) and a latent heat of fusion of
25 J/g. The specific heat capacity of wood is 1700 J/(kg
°C).
- Oscillation: You have been asked to evaluate the
design for a simple device to measure the mass of small
rocks on the Moon. The rock is attached to the free end
of a lightweight spring which horizontal. The surface on
which the rock slides is almost frictionless. You are
worried that the kinetic energy of the rock may make this
device dangerous in some situations. The device
specifications state that a 150 gram rock will execute
harmonic motion, with a frequency of 0.32 Hz, described
by x(t) = A sin (bt - 35º) when the rock has an initial
speed of 1.2 cm/s.
- Oscillations: You and some friends are waiting in
line for "The Mixer", a new carnival ride. The
ride begins with the car and rider (150 kg combined) at
the top of a curved track. At the bottom of the track is
a 50 kg block of cushioned material which is attached to
a horizontal spring whose other end is fixed in concrete.
The car slides down the track ending up moving
horizontally when it crashes into the cushioned block,
sticks to it, and oscillates at 3 repetitions in about 10
seconds. Your friends estimate that the car starts from a
height of around 10 feet. You decide to use your physics
knowledge to see if they are right. After the collision,
you notice that the spring compresses about 15 ft from
equilibrium.
- Traveling Waves: You've been hired as a technical
consultant to the Minneapolis police department to design
a radar detector-proof device that measures the speed of
vehicles. (i.e. one that does not rely on sending out a
radar signal that the car can detect.) You decide to
employ the fact that a moving car emits a variety of
characteristic sounds. Your idea is to make a very small
and low device to be placed in the center of the road
that will pick out a specific frequency emitted by the
car as it approaches and then measure the change in that
frequency as the car moves off in the other direction.
The device will then send the initial and final
frequencies to its microprocessor, and then use this data
to compute the speed of the vehicle. You are currently in
the process of writing a program for the chip in your new
device. To complete the program, you need a formula that
determines the speed of the car using the data received
by the microprocessor. You may also include in your
formula any physical constants that you might need.
Because your reputation as a designer is on the line, you
realize that you'll need find ways to check the validity
of your formula, even though it contains no numbers.
- Traveling Waves: You have the perfect summer job
with a team of marine biologists studying dolphin
communication off the coast of Hawaii. Massive boulders
on the ocean floor can interrupt the reception of
underwater sound waves from the dolphins. To reduce these
disruptions, your team has decided to put several
"transceivers" (a device that receives a
signal, amplifies the signal, and then transmits it) at
strategic locations on the ocean floor. A transceiver
will receive sound waves from a dolphin and then
retransmit them to the researchers on the ship. The
ship's receiver is on a long cable so that it is at
approximately the same depth as the dolphins. Because of
your physics background, you worry that the frequency
received at the moving ship will be different than that
emitted by the dolphin. To determine the size of this
effect, you assume that the ship is moving at 35km/h away
from the stationary transceiver. Meanwhile, the dolphin
is moving at 60km/h towards the transceiver and at an
angle of 63º to the ship's path when it emits a sound
frequency of 660Hz.
- Wave Equation: A friend of yours, a guitarist,
knows you are taking physics this semester and asks for
assistance in solving a problem. Your friend explains
that he keeps breaking repeatedly the low E string (640
Hz) on his Gibson "Les Paul" when he tunes-up
before a gig. The cost of buying new strings is getting
out of hand, so your friend is desperate to resolve his
Delia. Your friend tells you that the E string he is now
using is made of copper and has a diameter of 0.063
inches. You do some quick calculations and, given the
length of the neck of your friends guitar, estimate that
the wave speed on the E string is 1900 ft/s. While
reading about stringed instruments in the library, you
discover that most musical instrument strings will break
if they are subjected to a strain greater than about 2%.
How do you suggest your friend solve his problem?
- Standing Waves: Your friend, an artist, has been
thinking about an interesting way to display a new wind
sculpture she has just created. In order to create an
aural as well as visual effect, she would like to use the
wires needed to hang the sculpture as a sort of a string
instrument. She decides that with three wires and some
luck, the strings will sound a C-major dyad (C - 262Hz, G
- 392 Hz) when the wind blows (note: A dyad is part of a
chord.). Her basic design involves attaching a piece of
wire from two eye-hooks on the ceiling that are
approximately a foot-and-a-half apart and then hanging
the 50 pound sculpture from another wire attached to the
first wire forming a "y-shaped" arrangement.
Your friend tells you that she has been successful in
hanging the sculpture but not in "tuning" the
sound. Desperate for success, she knows you are taking
physics and asks for your help. Before you tackle the
analysis, you use your knowledge of waves to gather some
more information. You take a sample of the wire back to
your lab and measure its linear mass density to be 5.0
g/m. You also determine that wire is some sort of iron or
steel from its color. What is your advice?
- Standing Waves: You have a summer job in a
biomedical engineering laboratory studying the technology
to enhance hearing. You have learned that the human ear
canal is essentially an air filled tube approximately 2.7
cm long which is open on one end and closed on the other.
You wonder if there is a connection between hearing
sensitivity and standing waves so you calculate the
lowest three frequencies of the standing waves that can
exist in the ear canal. From your trusty Physics
textbook, you find that the speed of sound in air is 343
m/s.
- Standing Waves: You have joined a team designing a
new skyway that is to link the Physics Building to the
Mechanical Engineering Building. To make sure it will be
stable in gusts of wind, you need to find the lowest
frequency that sets up a standing wave in the skyway
structure. Your group has decided to make a scale model
of the skyway and put it into a wind tunnel to determine
the frequency. Unfortunately the wind tunnel cannot be
pulsed at a very low frequency. While the model is in the
wind tunnel you pulse the wind until you find a frequency
which sets up a standing wave in the model. You then
slowly increase the frequency until you get the next
standing wave pattern. Using the two frequencies you have
measured together with the length of the skyway model you
then calculate the lowest frequency which will set up a
standing wave.
- Energy, Frequency: You have an exciting summer job
working on an oil tanker in the waters of Alaska. Your
Captain knows that the ship is near an underwater
outcropping of land and wishes to avoid running into it.
He estimates that it is about 6 km straight ahead of the
ship and asks you to use the sonar to check how fast the
ship is approaching it. The ship's instruments tell you
the ship is moving through still water at a speed of 31
km/hr but the captain cannot take any chances. A sonar
signal is sent out with a frequency of 980 Hz, bounces
off the underwater obstacle, and is detected on the ship.
If the ship's speed indicator is correct, what frequency
should you detect? You use your trusty Physics text to
find the speed of sound in seawater is 1522 m/s.
- Rotations: You are helping a friend build an
experiment to test behavior modification techniques on
rats. She needs to build an obstacle that swings across a
path every 1.0 second. To keep the experiment as
inexpensive as possible, she wants to use a meter stick
as the swinging obstacle. She asks you to determine where
to drill a hole in the meter stick so that, when it is
hung by a nail through that hole, it will do the job for
small swings.
- Rotations: Your friend is trying to construct a
clock for a craft show and asks you for some advice. She
has decided to construct the clock with a pendulum. The
pendulum will be a very thin, very light wooden bar with
a thin, but heavy, brass ring fastened to one end. The
length of the rod is 80 cm and the diameter of the ring
is 10 cm. She is planning to drill a hole in the bar to
place the axis of rotation 15 cm from one end. She wants
you to tell her the period of this pendulum.
- Rotations: The child of a friend has asked you to
help with a school project. She wants to build a clock
from common materials. She has found a meter stick which
has a mass of 300g and asks you to determine where to
drill a hole in it so that when it is hung by a nail
through that hole it will be a pendulum with a period of
2.0 seconds for small oscillations. A quick calculation
tells you that the moment of inertia of the meter stick
about its center of mass is 1/12 of its mass times the
square of its length.
- Rotations: You have a part time job at a software
company that is currently under contract to produce a
program simulating accidents in the modern commuter
railroad station being planned for downtown. Your task is
to determine the response of a safety system to prevent a
railroad car from crashing into the station. In the
simulation, a coupling fails causing a passenger car to
break away from a train and roll into the station.
Furthermore, the brakes on the passenger car have failed.
It cannot stop on its own so it keeps on rolling. The
safety system at the end of the track is a large
horizontal spring with a hook that will grab onto the car
when it hits preventing the car from crashing into the
station platform. After the car hits the spring, your
program must calculate the frequency and amplitude of the
car's oscillation based on the specifications of the
passenger car, the specifications of the spring, and the
speed of the passenger car. In your simulation, the
wheels of the car are disks with a significant mass and a
moment of inertia half that of a ring of the same mass
and radius. At this stage of your simulation, you ignore
any energy dissipation in the car's axle or in the
flexing of the spring, and the mass of the spring.
- Rotations: You have been asked to help design an automated system for applying a resistive paint to plastic sheeting in order to mass produce containers to protect sensitive electronic components from static electric charges. The object used to apply the paint is a solid cylindrical roller. The roller is pushed back and forth over the plastic sheeting by a horizontal spring attached to a yoke, which in turn is attached to an axle through the center of the roller. The other end of the spring is attached to a fixed post. To apply the paint evenly, the roller must roll without slipping over the surface of the plastic. The machine simultaneously paints two narrow strips of plastic that lay side by side parallel to the axle of the roller. While the roller is in contact with one strip, a feed mechanism pulls the other strip forward to expose unpainted surface. In order to determine how fast the process can proceed, you have been assigned to calculate how the oscillation frequency of the roller depends on its mass, radius and the stiffness of the spring. You know that the moment of inertia of a solid cylinder with respect to an axis through its center is 1/2 that of a ring.
Electromagnetism problems:
The specific principles required are indicated in italics at the beginning of each problem.
- Electric Force: You and a friend are doing the
laundry when you unload the dryer and the discussion
comes around to static electricity. Your friend wants to
get some idea of the amount of charge that causes static
cling. You immediately take two empty soda cans, which
each have a mass of 120 grams, from the recycling bin.
You tie the cans to the two ends of a string (one to each
end) and hang the center of the string over a nail
sticking out of the wall. Each can now hangs straight
down 30 cm from the nail. You take your flannel shirt
from the dryer and touch it to the cans, which are
touching each other. The cans move apart until they hang
stationary at an angle of 10º from the vertical.
Assuming that there are equal amounts of charge on each
can, you now calculate the amount of charge transferred
from your shirt.
- Electric Force: You are part of a design team
assigned the task of making an electronic oscillator that
will be the timing mechanism of a micro-machine. You
start by trying to understand a simple model which is an
electron moving along an axis through the center and
perpendicular to the plane of a thin positively charged
ring. You need to determine how the oscillation frequency
of the electron depends on the size and charge of the
ring for displacements of the electron from the center of
the ring which are small compared to the size of the
ring. A team member suggests that you first determine the
acceleration of the electron along the axis as a function
of the size and charge of the ring and then use that
expression to determine the oscillation frequency of the
electron for small oscillations.
- Electric Force: You are spending the summer
working for a chemical company. Your boss has asked you
to determine where a chlorine ion of effective charge -e
would situate itself near a carbon dioxide ion. The
carbon dioxide ion is composed of 2 oxygen ions each with
an effective charge -2e and a carbon ion with an
effective charge +3e. These ions are arranged in a line
with the carbon ion sandwiched midway between the two
oxygen ions. The distance between each oxygen ion and the
carbon ion is 3.0 x 10-11 m. Assuming that the chlorine
ion is on a line that is perpendicular to the axis of the
carbon dioxide ion and that the line goes through the
carbon ion, what is the equilibrium distance for the
chlorine ion relative to the carbon ion on this line? For
simplicity, you assume that the carbon dioxide ion does
not deform in the presence of the chlorine ion. Looking
in your trusty physics textbook, you find the charge of
the electron is 1.60 x 10-19 C.
- Electric Force: You have been asked to review a
new apparatus, which is proposed for use at a new
semiconductor ion implantation facility. One part of the
apparatus is used to slow down He ions which are positive
and have a charge twice that of an electron (He++). This
part consists of a circular wire that is charged
negatively so that it becomes a circle of charge. The ion
has a velocity of 200 m/s when it passes through the
center of the circle of charge on a trajectory
perpendicular to the plane of the circle. The circle has
a charge of 8.0 µC and radius of 3.0 cm. The sample with
which the ion is to collide will be placed 2.5 mm from
the charged circle. To check if this device will work,
you decide to calculate the distance from the circle that
the ion goes before it stops. To do this calculation, you
assume that the circle is very much larger than the
distance the ion goes and that the sample is not in
place. Will the ion reach the sample? You look up the
charge of an electron and mass of the helium in your
trusty Physics text to be 1.6 x 10-19 C and 6.7 x 10-27
Kg.
- Electric Force: You've been hired to design the
hardware for an ink jet printer. You know that these
printers use a deflecting electrode to cause charged ink
drops to form letters on a page. The basic mechanism is
that uniform ink drops of about 30 microns radius are
charged to varying amounts after being sprayed out
towards the page at a speed of about 20 m/s. Along the
way to the page, they pass into a region between two
deflecting plates that are 1.6 cm long. The deflecting
plates are 1.0 mm apart and charged to 1500 volts. You
measure the distance from the edge of the plates to the
paper and find that it is one-half inch. Assuming an
uncharged droplet forms the bottom of the letter, how
much charge is needed on the droplet to form the top of a
letter 3 mm high (11 pt. type)?
- Electric Force: While working in a University
research laboratory your group is given the job of
testing an electrostatic scale, which is used to
precisely measure the weight of small objects. The device
consists of two very light but strong strings attached to
a support so that they hang straight down. An object is
attached to the other end of each string. One of the
objects has a very accurately known weight while the
other object is the unknown. A power supply is slowly
turned on to give each object an electric charge. This
causes the objects to slowly move away from each other.
When the power supply is kept at its operating value, the
objects come to rest at the same horizontal level. At
that time, each of the strings supporting them makes a
different angle with the vertical and that angle is
measured. To test your understanding of the device, you
first calculate the weight of an unknown sphere from the
measured angles and the weight of a known sphere. Your
known is a standard sphere with a weight of 2.000 N
supported by a string that makes an angle of 10.00º with
the vertical. The unknown sphere's string makes an angle
of 20.00º with the vertical. As a second step in your
process of understanding this device, estimate the net
charge on a sphere necessary for the observed deflection
if a string were 10 cm long. Make sure to give the
assumptions you used for this estimate.
- Electric Force: You and a friend have been given
the task of designing a display for the Physics building
that will demonstrate the strength of the electric force.
Your friend comes up with an idea that sounds neat
theoretically, but you're not sure it is practical. She
suggests you use an electric force to hold a marble in
place on a sloped plywood ramp. She would get the
electric force by attaching a uniformly charged
semicircular wire near the bottom of the ramp, laying the
wire flat on the ramp with each of its ends pointing
straight up the ramp. She claims that if the charges on
the marble and ring and the slope of the ramp are chosen
properly, the marble would be balanced midway between the
ends of the wire. To test this idea, you decide to
calculate the necessary amount of charge on the marble
for a reasonable ramp angle of 15 degrees and a
semicircle of radius 10 cm with a charge of 800
micro-coulombs. The marble would roll in a slot cut
lengthwise into the center of the ramp. The mass of the
lightest marble you can find is 25 grams.
- Electric Force, Gauss's Law: You have a great
summer job in a research laboratory with a group
investigating the possibility of producing power from
fusion. The device being designed confines a hot gas of
positively charged ions, called plasma, in a very long
cylinder with a radius of 2.0 cm. The charge density of
the plasma in the cylinder is 6.0 x 10-5 C/m3. Positively
charged Tritium ions are to be injected into the plasma
perpendicular to the axis of the cylinder in a direction
toward the center of the cylinder. Your job is to
determine the speed that a Tritium ion should have when
it enters the plasma cylinder so that its velocity is
zero when it reaches the axis of the cylinder. Tritium is
an isotope of Hydrogen with one proton and two neutrons.
You look up the charge of a proton and mass of the
tritium in your trusty Physics text to be 1.6 x 10-19 C
and 5.0 x 10-27 Kg.
- Electric and Gravitational Force: You and a friend
are reading a newspaper article about nuclear fusion
energy generation in stars. The article describes the
helium nucleus, made up of two protons and two neutrons,
as very stable so it doesn't decay. You immediately
realize that you don't understand why the helium nucleus
is stable. You know that the proton has the same charge
as the electron except that the proton charge is
positive. Neutrons you know are neutral. Why, you ask
your friend, don't the protons simply repel each other
causing the helium nucleus to fly apart? Your friend says
she knows why the helium nucleus does not just fly apart.
The gravitational force keeps it together, she says. Her
model is that the two neutrons sit in the center of the
nucleus and gravitationally attract the two protons.
Since the protons have the same charge, they are always
as far apart as possible on opposite sides of the
neutrons. What mass would the neutron have if this model
of the helium nucleus works? Is that a reasonable mass?
Looking in your physics book, you find that the mass of a
neutron is about the same as the mass of a proton and
that the diameter of a helium nucleus is 3.0 x 10-13 cm.
- Electric Field: You are helping to design a new
electron microscope to investigate the structure of the
HIV virus. A new device to position the electron beam
consists of a charged circle of conductor. This circle is
divided into two half circles separated by a thin
insulator so that half of the circle can be charged
positively and half can be charged negatively. The
electron beam will go through the center of the circle.
To complete the design your job is to calculate the
electric field in the center of the circle as a function
of the amount of positive charge on the half circle, the
amount of negative charge on the half circle, and the
radius of the circle.
- Electric Field: You have a summer job with the
telephone company working in a group investigating the
vulnerability of underground telephone lines to natural
disasters. Your task is to write a computer program which
will be used determine the possible harm to a telephone
wire from the high electric fields caused by lightning.
The underground telephone wire is supported in the center
of a long, straight steel pipe that protects it. When
lightening hits the ground it charges the steel pipe. You
are concerned that the resulting electric field might
harm the telephone wire. Since you know that the largest
field on the wire will be where it leaves the end of the
pipe, you calculate the electric field at that point as a
function of the length of the pipe, the radius of the
pipe, and the charge on the pipe.
The specific principles required are indicated in italics at the beginning of each problem.
- Electric Potential Energy: While sitting in a
restaurant with some friends, you notice that some
"neon" signs are different in color than
others. You know that these signs are essentially just
gas sealed in a glass tube. The gas, when heated
electrically, gives off light. One of your friends, who
is an art major, and makes such signs as sculpture, tells
you that the color of the light depends on which gas is
in the tube. All "neon" signs are not made
using neon gas. You know that the color of light tells
you its energy. Red light is a lower energy than blue
light. Since the light is given off by the atoms, which
make up the gas, the different colors must depend on the
structure of the different atoms of different gases.
Suppose that atomic structure is as given by the Bohr
theory which states that electrons are in uniform
circular motion around a heavy, motionless nucleus in the
center of the atom. This theory also states that the
electrons are only allowed to have certain orbits. When
an atom changes from one allowed orbit to another allowed
orbit, it radiates light as required by the conservation
of energy. Since only certain orbits are allowed, so the
theory goes, only light of certain energies (colors) can
be emitted. This seems to agree with the observations of
your artist friend. You decide to test the theory by
calculating the energy of light emitted by a simple atom
when an electron makes a transition from one allowed
orbit to another. You decide to consider hydrogen since
you know it is the simplest atom with one electron and a
nucleus consisting of one proton. You remember that the
proton has a mass 2000 times that of an electron. When
you get home you look in your textbook and find the
electron mass is 9 x 10-31 kg and its charge is 1.6 x
10-19 C. The radius of the smallest allowed electron
orbit for hydrogen is 0.5 x 10-10 meters, which
determines the normal size of the atom. The next allowed
orbit has a radius 4 times as large as the smallest
orbit.
- Electric Potential Energy: You have a great summer
job working in a cancer research laboratory. Your team is
trying to construct a gas laser that will give off light
of an energy that will pass through the skin but be
absorbed by cancer tissue. You know that an atom emits a
photon (light) when an electron goes from a higher energy
orbit to a lower energy orbit. Only certain orbits are
allowed in a particular atom. To begin the process, you
calculate the energy of photons emitted by a Helium ion
in which the electron changes from an orbit with a radius
of 0.30 nanometers to another orbit with a radius of 0.20
nanometers. A nanometer is 10-9 m. The helium nucleus
consists of two protons and two neutrons.
- Electric Potential Energy: Your job is to evaluate
an electron gun designed to initiate an electron beam.
The electrons have a 20 cm path from the heating element,
which emits them to the end of the gun. This path is
through a very good vacuum. For most applications, the
electrons must reach the end of the gun with a speed of
at least 107 m/s. After leaving the heating element, the
electrons pass through a 5.0 mm diameter hole in the
center of a 3.0 cm diameter charged circular disk. The
disk's charge density is kept at 3.0 µC/m2. The heating
element is a spherical electrode 0.10 mm in diameter that
is kept at a very high charge of -0.10C. There is 1.0 cm
between the heating element and the hole in the disk.
Your first step is to determine if the electrons are
going fast enough. Your boss has pointed that the hole in
the disk is too large to ignore in your calculations.
Using your physics text you find that the mass of the
electron is 9.11 x 10-31 kg.
- Electric Potential Energy - Gauss's Law: You have
landed a summer job working with an Astrophysics group
investigating the origin of high-energy particles in the
galaxy. The group you are joining has just discovered a
large spherical nebula with a radius 1.2 million km. The
nebula consists of about 5 x 1010 hydrogen nuclei
(protons) which appear to be uniformly distributed in the
shape of a sphere. At the center of this sphere of
positive charge is a very small neutron star. Your group
had detected electrons emerging from the nebula. A friend
of yours has a theory that the electrons are coming from
the neutron star. To test that theory, she asks you to
calculate the minimum speed that an electron would need
to start from the neutron star and just make it to
outside the nebula. From the inside cover of your trusty
physics text you find that the charge of a proton (and an
electron) is 1.6 x 10-19 C, the mass of the proton is 1.7
x 10-27 kg, and the mass of the electron is 9.1 x 10 -31
kg.
- Electric Potential Energy, Gauss's Law: You are
working in cooperation with the Public Health department
to design an electrostatic trap for particles from auto
emissions. The average particle enters the device and is
exposed to ultraviolet radiation that knocks off
electrons so that it has a charge of +3.0 x 10-8 C. This
average particle is then moving at a speed of 900 m/s and
is 15 cm from a very long negatively charged wire with a
linear charge density of -8.0 x 10-6 C/m. The detector
for the particle is located 7.0 cm from the wire. In
order to design the proper kind of detector, your
colleagues need to know the speed that an average
emission particle will have if it hits the detector. They
tell you that an average emission particle has a mass of
6.0 x 10-9 kg.
- Electric Potential Energy, Heat Energy (Heat Capacity,
Latent Heat): You are reading a newspaper
report of a lightning strike in Jackson, Wyoming. Two men
were sitting at a table outside a small cafe on a
beautiful 30 oC day when a thunderstorm approached.
Suddenly, a bolt of lightning struck a large aspen tree
near their table. Needless to say, the men were very
startled. One of the men remarked, "It just about
scared the espresso out of me." They reported that
when the bolt hit the tree and there was a loud hiss and
a release of much steam from the tree. The lightning had
boiled away some of the tree's sap. You are curious, and
wonder how much water could be evaporated in this manner.
So you study your physics book and make a few estimates
and assumptions. You estimate that the electric potential
difference between the tree and the thunderhead cloud was
about 108 volts, and the amount of charge released by the
bolt was about 50 Coulombs. You also assume that about 1%
of the electrical energy was actually transferred into
the sap, which is essentially water. The specific heat
capacity of water is 4200 J/(kg oC) and its heat of
vaporization is 2.3 x 106 J/kg.
- Electric Potential Energy, Gravitational Force:
NASA has asked your team of rocket scientists about the
feasibility of a new satellite launcher that will save
rocket fuel. NASA's idea is basically an electric
slingshot that consists of 4 electrodes arranged in a
horizontal square with sides of length d at a height h
above the ground. The satellite is then placed on the
ground aligned with the center of the square. A power
supply will provide each of the four electrodes with a
charge of +Q/4 and the satellite with a charge -Q. When
the satellite is released from rest, it moves up and
passes through the center of the square. At the instant
it reaches the square's center, the power supply is
turned off and the electrodes are grounded, giving them a
zero electric charge. To test this idea, you decide to
use energy considerations to calculate how big Q will
have to be to get a 100 kg satellite to a sufficient
orbit height. Assume that the satellite starts from 15
meters below the square of electrodes and that the sides
of the square are each 5 meters. In your physics text you
find the mass of the Earth to be 6.0 x 1024 kg.
- Electric Potential Energy, Mechanical Energy: You
have been able to get a part-time job in a University
laboratory. The group is planning a set of experiments to
study the forces between nuclei in order to understand
the energy output of the Sun. To do this experiment, you
shoot alpha particles from a Van de Graaf accelerator at
a sheet of lead. The alpha particle is the nucleus of a
helium atom and is made of 2 protons and 2 neutrons. The
lead nucleus is made of 82 protons and 125 neutrons. The
mass of the neutron is almost the same as the mass of a
proton. To assure that you are actually studying the
effects of the nuclear force, an alpha particle should
come into contact with a lead nucleus. Assume that both
the alpha particle and the lead nucleus have the shape of
a sphere. The alpha particle has a radius of 1.0 x 10-13
cm and the lead nucleus has a radius 4 times larger. Your
boss wants you to make two calculations:
(a) What is the minimum speed of such an alpha particle if the lead nucleus is fixed at rest?
(b) What is the potential difference between the two ends of the Van de Graaf accelerator if the alpha particle starts from rest at one end (from a bottle of helium gas)?
- It's a cool day, about 10 oC, so you plan to make about
5.0 kg of clear soup using your slow cooking crockpot. To
decide whether the soup will be ready for dinner, you
estimate how long it will take before the soup gets to
its boiling point. Before adding the ingredients, you
turn the crockpot over and read that it is a 200-ohm
device that operates at 120 volts. Since your soup is
mostly water, you assume it has the same thermal
properties as water, so its specific heat capacity is
4200 J/(kg oC) and its heat of vaporization is 2.3 x 106
J/kg.
- You are working with a company that has the contract to
design a new, 700-foot high, 50-story office building in
Minneapolis. Your boss suddenly bursts into your office.
She has been talking with an engineer who told her that
when the elevator is operating at maximum speed, it would
take the 6500-lb loaded elevator one minute to rise 20
stories. She thinks this is too long a time for these
busy executives to spend in an elevator after returning
from lunch at the Minneapolis Athletic Club. She wants
you to buy a bigger power supply for the elevator. You
look up the specifications for the new supply and find
that it is the same as the old one except that it
operates at twice the voltage. Your boss's assistant
argues that the operating expenses of the new power
supply will be much more than the old one. Your boss
wants you to determine if this is correct. You estimate
that while the elevator runs at maximum speed, the whole
system, including the power supply, is 60% efficient. The
cost of electricity is $0.06 per kilowatt-hour
(commercial rate).
- You have finally graduated from college and found a job
with the Washington State Agricultural Concerns Group.
Farmers and fishermen are concerned that the rate that
water flows in the Columbia river, which is controlled by
dams, will not be adequate for both irrigation needs and
salmon spawning. The dams control the river's flow rate
to produce most of the electrical power for cities along
the West Coast. Your group leader assigns you the task of
calculating the volume of water per second (flow rate)
which normally would flow through the Grand Coulee Dam,
the largest on the Columbia River. She tells you that
this dam typically generates 2000 megawatts (MW) of power
and is 50% efficient in converting the water's energy to
electrical energy. The dam is 170 meters high ,and the
water is kept in a lake 10 meters below the top of the
dam. The Columbia River is 170 meters wide at the dam.
The density of water is 1.00 g/cm3.
- Ohm's Law: Because of your physics background, you
landed a summer job as an assistant technician for a
telephone company in California. During a recent
earthquake, a 1.0-mile long underground telephone line is
crushed at some point. This telephone line is made up of
two parallel copper wires of the same diameter and same
length, which are normally not connected. At the place
where the line is crushed, the two wires make contact.
Your boss wants you to find this place so that the wire
can be dug up and fixed. You disconnect the line from the
telephone system by disconnecting both wires of the line
at both ends. You then go to one end of the line and
connect one terminal of a 6.0-V battery to one wire, and
the other terminal of the battery to one terminal of an
ammeter (which has essentially zero resistance). When the
other terminal of the ammeter is connected to the other
wire, the ammeter shows that the current through the wire
is 1 A. You then disconnect everything and travel to the
other end of the telephone line, where you repeat the
process and find a current of 1/3 A.
- Ohm's Law: You have a summer job in the
University ecology lab. Your supervisor asks you to
duplicate an electromagnet that she has borrowed. She
tells you that this electromagnet is made by wrapping a
wire many times around a piece of iron and provides you
with all the parts, the same type of wire of the same
diameter and an identical iron core. What you need to
know is how much wire to wrap around the iron.
Unfortunately, you cannot simply unwrap the wire from the
borrowed magnet because that will destroy it. On the side
of the electromagnet, it tells you that when a potential
difference of 12 V is put across the ends of its wire,
there is a current of 0.06 A through the wire. With a
brilliant flash of insight, you realize that the
cross-sectional area and the conductivity is the same for
both the magnet's wire and the wire you have, so you can
find the length with a simple experiment. You cut off a
100-foot piece of identical wire from your supply, attach
it to a 1.5-V flashlight battery and measure a current of
0.10 A through that wire. Eureka! you can now find the
length of the magnet's wire.
- Electric Power: You and a friend are studying for
an exam and the session goes until the early morning. At
about 4 am you decide to cook some breakfast. Despite
being sleepy you've got the coffee perking. Now you want
to make some waffles but you realize there might be a
problem. The 1000-watt waffle iron and the 600-watt
coffee maker are plugged into the 110 V kitchen
electrical outlets. If you plug in your 700-watt blender,
will you overload the 20 A circuit breaker? The circuit
breaker protects those kitchen circuit wires that have
the most current from carrying too much current. You are
trying to figure out how the electrical outlets are
connected together in a circuit when your friend reminds
you that when you disconnect the coffeepot, the waffle
iron stays on. Now everything is clear.
- Electric Power: You and a friend are studying for
a final and the session goes until the early morning.
About 4 AM you decide to cook some breakfast. Despite
being sleepy, things are going well. The waffles are
cooking and the coffee is perking. Should you make some
toast now? The 1000-watt waffle iron and the 600-watt
coffee maker are plugged into kitchen wall electrical
outlets. You will also use a kitchen wall outlet for the
toaster. The kitchen wall outlets are all part of the
same 110-V circuit which has a 20-A circuit breaker (with
negligible resistance) to protect the wire carrying the
largest current from getting too hot. (Some homes have
fuses to do the same job). You know that if you plug in
too many appliances you will overload the circuit
breaker. The toaster label says that its power output is
700 watts.
- Electric Power: As a member of the safety group
for the space shuttle scientific program, you have been
asked to evaluate an electronics design change. In order
to improve the reliability of a circuit to be used in the
next shuttle flight, the experimental design team has
suggested adding a second 12 V battery to the circuit.
The equivalent resistances of the proposed design are
shown below. You are worried about the heat generated by
the device with the 20 ohm resistance since it will be
located next to a sensitive low temperature experiment so
you do the appropriate calculation.
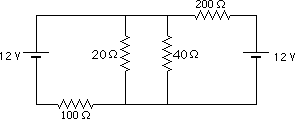
-
Electric Power:
As part of your summer job as a design engineer
at an electronics company, you have been asked to
inspect the circuit shown below. The resistors
are rated at 0.5 Watts, which means they burn-up
if more than 0.5 Watts of power passes through
them. Will the 100W resistor in the circuit
burn-up?
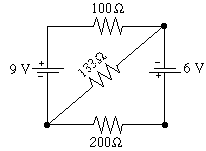
- Electric Power: While trying to find the power
ratings of your appliances you find their circuit
diagrams. Looking them over, your friend believes there
must be a typo in the circuit diagram of your toaster.
The heating element that toasts the bread is listed as
having a resistance of 5 ohms. A variable resistor, which
is changed by a knob on front of the toaster, has a range
of from 2 to 20 ohms. Your friend feels that an element
with this resistance will not toast bread properly. Based
on the circuit diagram, given below, you decide to
calculate the maximum power output by the heating
element.
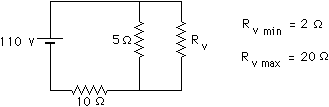
- Magnetic Force: You are working on a project to
make a more efficient engine. Your team is investigating
the possibility of making electrically controlled valves
that open and close the input and exhaust openings for an
internal combustion engine. Your assignment is to
determine the stability of the valve by calculating the
force on each of its sides and the net force on the
valve. The valve is made of a thin but strong rectangular
piece of non-magnetic material that has a loop of current
carrying wire along its edges. The rectangle is 0.35 cm x
1.83 cm. The valve is placed in a uniform magnetic field
of 0.15 T such that the field lies in the plane of the
valve and is parallel to the short sides of the
rectangle. The region with the magnetic field is slightly
larger than the valve. When a switch is closed, a 1.7 A
current enters the short side of the rectangle on one
side of the valve and leaves on the opposite side. To
give different currents through the wires along the long
sides of the valve, a resistor is inserted into the wire
on each of these sides. The value of the resistor on one
side is twice that on the other side.
- Magnetic Force: You have landed a great summer job
in the medical school assisting in a research group
investigating short lived radioactive isotopes which
might be useful in fighting cancer. Your group is working
on a way of transporting alpha particles (Helium nuclei)
from where they are made to another room where they will
collide with other material to form the isotopes. Since
the radioactive isotopes are not expected to live very
long, it is important to know precisely how much time it
will take to transport the alpha particles. Your job is
to design that part of the transport system which will
deflect the beam of alpha particles (m = 6.64 x 10-27 kg,
q = 3.2 x 10-19 C) through an angle of 90o by using a
magnetic field. The beam will be traveling horizontally
in an evacuated tube. At the place the tube is to make a
90o turn you decide to put a dipole magnet which provides
a uniform vertical magnetic field of 0.030 T. Your design
has a tube of the appropriate shape between the poles of
the magnet. Before you submit your design for
consideration, you must determine how long the alpha
particles will spend in the uniform magnetic field in
order to make the 90o-turn.
- Magnetic Force: You've just learned about the
earth's magnetic field and how a compass works and you
are relaxing in front of the TV. Tired of your show, you
think about how the picture tube works in relation to
what you have learned. In a typical color picture tube
for a TV, the electrons are boiled off of a cathode at
the back of the tube and are accelerated through about
20,000 volts towards the picture tube screen. On the
screen is a grid of ``color dots'' about 1/100 inch
apart. When the electrons hit them, the dots scintillate
their appropriate colors producing the color picture.
Without taking apart the set, you determine whether the
manufacturer needed to shield the color picture tube from
the earth's magnetic field?
-
Magnetic Field
(Biot-Savert Law): You are continually having
troubles with the CRT screen of your computer and
wonder if it is due to magnetic fields from the
power lines running in your building. A blueprint
of the building shows that the nearest power line
is as shown below. Your CRT screen is located at
point P. Calculate the magnetic field at P as a
function of the current I and the distances a and
b. Segments BC and AD are arcs of concentric
circles. Segments AB and DC are straight-line
segments.
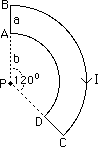
- Magnetic Field - Amphere's Law: While studying
intensely for your physics final you decide to take a
break and listen to your stereo. As you unwind, your
thoughts drift to newspaper stories about the dangers of
household magnetic fields on the body. You examine your
stereo wires and find that most of them are coaxial
cable, a thin conducting wire at the center surrounded by
an insulator, which is in turn surrounded by a conducting
shell. The inner wire and the conducting shell are both
part of the circuit with the same current (I) passing
through both, but in opposite directions. As a way to
practice for your physics final you decide to calculate
the magnetic field in the insulator, and outside the
coaxial cable as a function of the current and the
distance from the center of the cable. As an additional
challenge to yourself, you calculate what the magnetic
field would be (as a function of the current and the
distance from the center of the cable) inside the outer
conducting shell of the coaxial cable. For this you
assume that the inner radius of the conducting shell is
R1 and the outer radius is R2.
- Magnetic Force - Faraday's Law: You have a summer
job working at a company developing systems to safely
lower large loads down ramps. Your team is investigating
a magnetic system by modeling it in the laboratory. The
safety system is a conducting bar that slides on two
parallel conducting rails that run down the ramp. The bar
is perpendicular to the rails and is in contact with
them. At the bottom of the ramp, the two rails are
connected together. The bar slides down the rails through
a vertical uniform magnetic field. The magnetic field is
supposed to cause the bar to slide down the ramp at a
constant velocity even when friction between the bar and
the rails is negligible. Before setting up the laboratory
model, your task is to calculate the constant velocity of
the bar sliding down the ramp on rails in a vertical
magnetic field as a function of the mass of the bar, the
strength of the magnetic field, the angle of the ramp
from the horizontal, the length of the bar which is the
same as the distance between the tracks, and the
resistance of the bar. Assume that all of the other
conductors in the system have a much smaller resistance
than the bar.
Unsorted Problems
(note: These problems have not necessarily been tested at the University of Minnesota)
This page under construction...check back soon.
Submit your own Context-Rich Problems
PER
Context-rich Problems
- Home Page
- Examples
- Comparison to Traditional Problems
- Creating Context Rich Problems
- Rating Difficulty
- Coding Student Solutions (2005)
- Problem-solving Rubric (current)
- On-line Archive